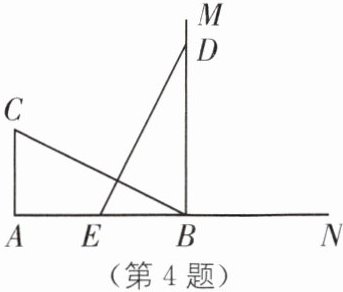
4. 分类讨论思想 如图,CA⊥AB,垂足为 A,射线 BM⊥AB,垂足为 B,AB= 12 cm,AC= 6 cm. 动点 E 从点 A 出发以 3 cm/s 的速度沿射线 AN 运动,动点 D 在射线 BM 上,随着点 E 运动而运动,始终保持 ED= CB. 若点 E 的运动时间为 t s(t>0),则当 t 为多少时,△DEB 与△BCA 全等?

答案:4. ①当点 E 在线段 AB 上,且 AC=BE 时,△ACB≌△BED,
∵AC=6 cm,
∴BE=6 cm,
∴AE=12 - 6 = 6(cm),
∴点 E 的运动时间为 6÷3 = 2(s);
②当 E 在射线 BN 上,AC=BE 时,
∵AC=BE=6 cm,
∴AE=12 + 6 = 18(cm),
∴点 E 的运动时间为 18÷3 = 6(s);
③当 E 在线段 AB 上,AB=EB 时,△ACB≌△BDE,这时 E 在 A 点未动,因此时间为 0 s(舍去此情况);
④当 E 在射线 BN 上,AB=EB 时,△ACB≌△BDE,
AE=12 + 12 = 24(cm),
∴点 E 的运动时间为 24÷3 = 8(s).
综上,t 的值为 2 或 6 或 8.
∵AC=6 cm,
∴BE=6 cm,
∴AE=12 - 6 = 6(cm),
∴点 E 的运动时间为 6÷3 = 2(s);
②当 E 在射线 BN 上,AC=BE 时,
∵AC=BE=6 cm,
∴AE=12 + 6 = 18(cm),
∴点 E 的运动时间为 18÷3 = 6(s);
③当 E 在线段 AB 上,AB=EB 时,△ACB≌△BDE,这时 E 在 A 点未动,因此时间为 0 s(舍去此情况);
④当 E 在射线 BN 上,AB=EB 时,△ACB≌△BDE,
AE=12 + 12 = 24(cm),
∴点 E 的运动时间为 24÷3 = 8(s).
综上,t 的值为 2 或 6 或 8.
5. 一线三垂直模型 在△ABC 中,∠ACB= 90°,AC= BC,直线 MN 经过点 C,且 AD⊥MN 于点 D,BE⊥MN 于点 E.
(1)当直线 MN 绕点 C 旋转到图(1)的位置时,求证:①△ADC≌△CEB;②DE= AD+BE.
(2)当直线 MN 绕点 C 旋转到图(2)的位置时,(1)中的结论还成立吗?若成立,请给出证明;若不成立,请说明理由.
 精题详解
精题详解
(1)当直线 MN 绕点 C 旋转到图(1)的位置时,求证:①△ADC≌△CEB;②DE= AD+BE.
(2)当直线 MN 绕点 C 旋转到图(2)的位置时,(1)中的结论还成立吗?若成立,请给出证明;若不成立,请说明理由.
 精题详解
精题详解答案:5.
(1)①
∵∠ACD+∠BCE=90°,∠DAC+∠ACD=90°,
∴∠DAC=∠ECB.
在△ADC 和△CEB 中,{∠ADC=∠CEB=90°,∠DAC=∠ECB,AC=CB}
∴△ADC≌△CEB(AAS).
②
∵△ADC≌△CEB,
∴CD=BE,AD=CE.
∴DE=CE+CD=AD+BE.
(2)△ADC≌△CEB 成立,DE=AD+BE 不成立,此时应有 DE=AD - BE.理由如下:
∵∠ACD+∠BCE=90°,∠DAC+∠ACD=90°,
∴∠DAC=∠BCE.
又 AC=BC,∠ADC=∠BEC=90°,
∴△ADC≌△CEB(AAS).
∴CD=BE,AD=CE.
∴DE=AD - BE.
(1)①
∵∠ACD+∠BCE=90°,∠DAC+∠ACD=90°,
∴∠DAC=∠ECB.
在△ADC 和△CEB 中,{∠ADC=∠CEB=90°,∠DAC=∠ECB,AC=CB}
∴△ADC≌△CEB(AAS).
②
∵△ADC≌△CEB,
∴CD=BE,AD=CE.
∴DE=CE+CD=AD+BE.
(2)△ADC≌△CEB 成立,DE=AD+BE 不成立,此时应有 DE=AD - BE.理由如下:
∵∠ACD+∠BCE=90°,∠DAC+∠ACD=90°,
∴∠DAC=∠BCE.
又 AC=BC,∠ADC=∠BEC=90°,
∴△ADC≌△CEB(AAS).
∴CD=BE,AD=CE.
∴DE=AD - BE.