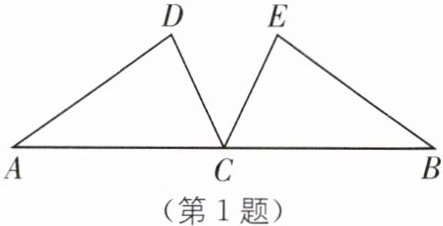
1.(2024·西藏中考)如图,点 C 是线段 AB 的中点,AD= BE,∠A= ∠B.求证:∠D= ∠E.

答案:
∵点C是线段AB的中点,
∴AC=BC.
在△DAC和△EBC中,{AD=BE,∠A=∠B,AC=BC}
∴△DAC≌△EBC(SAS),
∴∠D=∠E.
归纳总结 本题考查了全等三角形的判定与性质,熟练掌握全等三角形的判定和性质定理是解题的关键.
∵点C是线段AB的中点,
∴AC=BC.
在△DAC和△EBC中,{AD=BE,∠A=∠B,AC=BC}
∴△DAC≌△EBC(SAS),
∴∠D=∠E.
归纳总结 本题考查了全等三角形的判定与性质,熟练掌握全等三角形的判定和性质定理是解题的关键.
2.(2023·乐山中考)如图,已知 AB 与 CD 相交于点 O,AC//BD,AO= BO,求证:AC= BD.


答案:
∵AC//BD,
∴∠A=∠B,∠C=∠D.
在△AOC和△BOD中,{∠C=∠D,∠A=∠B,AO=BO}
∴△AOC≌△BOD(AAS),
∴AC=BD.
∵AC//BD,
∴∠A=∠B,∠C=∠D.
在△AOC和△BOD中,{∠C=∠D,∠A=∠B,AO=BO}
∴△AOC≌△BOD(AAS),
∴AC=BD.
3. 实验班原创 如图,已知△ABC 和△CDE 均是直角三角形,∠ACB= ∠CED= 90°,AC= CE,AB⊥CD 于点 F.
(1)求证:△ABC≌△CDE;
(2)若点 B 是 EC 的中点,DE= 12 cm,求 AC 的长.

(1)求证:△ABC≌△CDE;
(2)若点 B 是 EC 的中点,DE= 12 cm,求 AC 的长.

答案:
(1)
∵AB⊥CD,
∴∠AFC=90°,
∴∠BAC+∠ACF=90°.
∵∠ACE=90°,即∠DCE+∠ACF=90°,
∴∠BAC=∠DCE.
在△ABC和△CDE中,{∠BAC=∠DCE,AC=CE,∠ACB=∠CED}
∴△ABC≌△CDE(ASA).
(2)由
(1)知,△ABC≌△CDE,
∴BC=DE=12cm.
∵点B是EC的中点,
∴CE=2BC=24cm,
∴AC=CE=24cm.
(1)
∵AB⊥CD,
∴∠AFC=90°,
∴∠BAC+∠ACF=90°.
∵∠ACE=90°,即∠DCE+∠ACF=90°,
∴∠BAC=∠DCE.
在△ABC和△CDE中,{∠BAC=∠DCE,AC=CE,∠ACB=∠CED}
∴△ABC≌△CDE(ASA).
(2)由
(1)知,△ABC≌△CDE,
∴BC=DE=12cm.
∵点B是EC的中点,
∴CE=2BC=24cm,
∴AC=CE=24cm.
4. 如图,点 B,C,D,F 在一条直线上,FD= BC,DE= CA,EF= AB.求证:EF//AB.


答案:在△FDE和△BCA中,{FD=BC,DE=CA,EF=AB}
∴△FDE≌△BCA(SSS),
∴∠F=∠B,
∴EF//AB.
∴△FDE≌△BCA(SSS),
∴∠F=∠B,
∴EF//AB.
5.(2025·扬州广陵区期中)如图,AB= CD,DE⊥AC,BF⊥AC,E,F 是垂足,DE= BF.求证:
(1)AE= CF;
(2)AB//CD.

(1)AE= CF;
(2)AB//CD.

答案:
(1)
∵DE⊥AC,BF⊥AC,
∴∠DEC=∠BFA=90°,
∴在Rt△ABF和Rt△CDE中,{AB=CD,BF=DE}
∴△ABF≌△CDE(HL),
∴AF=CE,
即AF - EF=CE - EF,
∴AE=CF.
(2)
∵△ABF≌△CDE,
∴∠A=∠C,
∴CD//AB.
(1)
∵DE⊥AC,BF⊥AC,
∴∠DEC=∠BFA=90°,
∴在Rt△ABF和Rt△CDE中,{AB=CD,BF=DE}
∴△ABF≌△CDE(HL),
∴AF=CE,
即AF - EF=CE - EF,
∴AE=CF.
(2)
∵△ABF≌△CDE,
∴∠A=∠C,
∴CD//AB.
6. 中考新考法 满足结论的条件开放 如图,AD,A'D'分别为钝角三角形 ABC 和钝角三角形 A'B'C'的边 BC,B'C'上的高,且 AB= A'B',AD= A'D'.请你补充一个条件______ (只需写出一个你认为适当的条件),使得△ABC≌△A'B'C',并加以证明.


BC=B'C'
答案:答案不唯一,如可添加条件BC=B'C'. 证明如下:
∵AD,A'D'分别为边BC,B'C'上的高,
∴∠ADB=∠A'D'B'=90°.
在Rt△ADB和Rt△A'D'B'中,{AB=A'B',AD=A'D'}
∴Rt△ADB≌Rt△A'D'B'(HL),
∴∠B=∠B'.
在△ABC和△A'B'C'中,{AB=A'B',∠B=∠B',BC=B'C'}
∴△ABC≌△A'B'C'(SAS).
易错警示 本题考查了全等三角形的判定及性质,添加条件时注意:AAA,SSA不能判定两个三角形全等.
∵AD,A'D'分别为边BC,B'C'上的高,
∴∠ADB=∠A'D'B'=90°.
在Rt△ADB和Rt△A'D'B'中,{AB=A'B',AD=A'D'}
∴Rt△ADB≌Rt△A'D'B'(HL),
∴∠B=∠B'.
在△ABC和△A'B'C'中,{AB=A'B',∠B=∠B',BC=B'C'}
∴△ABC≌△A'B'C'(SAS).
易错警示 本题考查了全等三角形的判定及性质,添加条件时注意:AAA,SSA不能判定两个三角形全等.