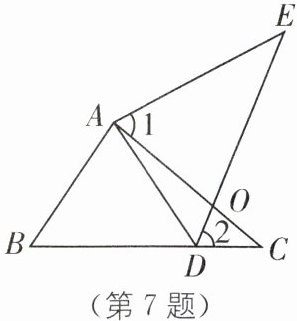
7.(2024·苏州吴中区期中)如图,点 D 在 BC 上,AC 与 DE 相交于点 O,∠1= ∠2,AE= AC,下面三个条件:
①AB= AD;②BC= DE;③∠E= ∠C.
请你从①②③中选一个条件,使△ABC≌△ADE.
(1)你添加的条件是
(2)添加了条件后,请证明△ABC≌△ADE.
(2)
∵∠1=∠2,∠AOE=∠COD,
∴∠E=∠C.
在△ABC和△ADE中,{AC=AE,∠C=∠E,BC=DE}
∴△ABC≌△ADE(SAS).
①AB= AD;②BC= DE;③∠E= ∠C.
请你从①②③中选一个条件,使△ABC≌△ADE.
(1)你添加的条件是
②
(填序号);(2)添加了条件后,请证明△ABC≌△ADE.

(2)
∵∠1=∠2,∠AOE=∠COD,
∴∠E=∠C.
在△ABC和△ADE中,{AC=AE,∠C=∠E,BC=DE}
∴△ABC≌△ADE(SAS).
答案:
(1)②
(2)
∵∠1=∠2,∠AOE=∠COD,
∴∠E=∠C.
在△ABC和△ADE中,{AC=AE,∠C=∠E,BC=DE}
∴△ABC≌△ADE(SAS).
知识拓展 本题考查了三角形全等的判定方法,判定两个三角形全等的一般方法有SSS,SAS,ASA,AAS,HL(直角三角形).
(1)②
(2)
∵∠1=∠2,∠AOE=∠COD,
∴∠E=∠C.
在△ABC和△ADE中,{AC=AE,∠C=∠E,BC=DE}
∴△ABC≌△ADE(SAS).
知识拓展 本题考查了三角形全等的判定方法,判定两个三角形全等的一般方法有SSS,SAS,ASA,AAS,HL(直角三角形).
8. 一题多问 (2025·南京联合体期中)如图,在△ABC 与△ADE 中,点 C 在 DE 上,且 AB= AD,AC= AE,∠BAD= ∠CAE.
(1)求证:△ABC≌△ADE;
(2)点 F 在 BC 上,若 AF= AC,求证:△ABF≌△ADC.

(1)求证:△ABC≌△ADE;
(2)点 F 在 BC 上,若 AF= AC,求证:△ABF≌△ADC.

答案:
(1)
∵∠BAD=∠CAE,
∴∠BAD+∠DAC=∠CAE+∠DAC,
∴∠BAC=∠DAE.
在△ABC和△ADE中,{AB=AD,∠BAC=∠DAE,AC=AE}
∴△ABC≌△ADE(SAS).
(2)
∵△ABC≌△ADE,
∴∠B=∠D,∠E=∠ACF,BC=DE.
由AC=AE,易得∠E=∠ACE.
由AF=AC,易得∠AFC=∠ACF,
∴∠E=∠ACE=∠AFC=∠ACF.
在△AFC和△AEC中,{∠AFC=∠E,∠ACF=∠ACE,AC=AC}
∴△AFC≌△AEC(AAS),
∴CF=CE,
∴BC - CF=DE - CE,
∴BF=CD.
在△ABF和△ADC中,{AB=AD,∠B=∠D,BF=DC}
∴△ABF≌△ADC(SAS).
(1)
∵∠BAD=∠CAE,
∴∠BAD+∠DAC=∠CAE+∠DAC,
∴∠BAC=∠DAE.
在△ABC和△ADE中,{AB=AD,∠BAC=∠DAE,AC=AE}
∴△ABC≌△ADE(SAS).
(2)
∵△ABC≌△ADE,
∴∠B=∠D,∠E=∠ACF,BC=DE.
由AC=AE,易得∠E=∠ACE.
由AF=AC,易得∠AFC=∠ACF,
∴∠E=∠ACE=∠AFC=∠ACF.
在△AFC和△AEC中,{∠AFC=∠E,∠ACF=∠ACE,AC=AC}
∴△AFC≌△AEC(AAS),
∴CF=CE,
∴BC - CF=DE - CE,
∴BF=CD.
在△ABF和△ADC中,{AB=AD,∠B=∠D,BF=DC}
∴△ABF≌△ADC(SAS).
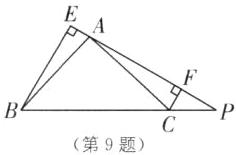
9. 一线三等角模型 如图,在△ABC 中,已知∠BAC= 90°,AB= AC,点 P 为边 BC 上一动点(BP<CP),分别过点 B,C 作 BE⊥AP 于点 E,CF⊥AP 于点 F.
(1)求证:EF= CF-BE.
(2)若点 P 为 BC 延长线上一点,其他条件不变,则线段 BE,CF,EF 是否存在某种确定的数量关系?画图并直接写出你的结论.

(1)求证:EF= CF-BE.
(2)若点 P 为 BC 延长线上一点,其他条件不变,则线段 BE,CF,EF 是否存在某种确定的数量关系?画图并直接写出你的结论.

答案:
(1)
∵BE⊥AP,CF⊥AP,
∴∠E=∠CFA=90°,
∴∠FAC+∠ACF=90°.
∵∠BAC=90°,
∴∠BAE+∠FAC=90°,
∴∠BAE=∠ACF.
在△ABE和△CAF中,{∠E=∠CFA,∠BAE=∠ACF,AB=CA}
∴△ABE≌△CAF(AAS),
∴AE=CF,BE=AF.
∵EF=AE - AF,
∴EF=CF - BE.
(2)EF=BE+CF. 理由如下:
如图,
∵BE⊥AP,CF⊥AP,
∴∠E=∠AFC=90°,
∴∠FAC+∠ACF=90°.
∵∠BAC=90°,
∴∠BAE+∠FAC=90°,
∴∠BAE=∠ACF.
在△ABE和△CAF中,{∠E=∠AFC,∠BAE=∠ACF,AB=CA}
∴△ABE≌△CAF(AAS),
∴AE=CF,BE=AF.
∵EF=AF+AE,
∴EF=BE+CF.
(1)
∵BE⊥AP,CF⊥AP,
∴∠E=∠CFA=90°,
∴∠FAC+∠ACF=90°.
∵∠BAC=90°,
∴∠BAE+∠FAC=90°,
∴∠BAE=∠ACF.
在△ABE和△CAF中,{∠E=∠CFA,∠BAE=∠ACF,AB=CA}
∴△ABE≌△CAF(AAS),
∴AE=CF,BE=AF.
∵EF=AE - AF,
∴EF=CF - BE.
(2)EF=BE+CF. 理由如下:
如图,
∵BE⊥AP,CF⊥AP,
∴∠E=∠AFC=90°,
∴∠FAC+∠ACF=90°.
∵∠BAC=90°,

∴∠BAE+∠FAC=90°,
∴∠BAE=∠ACF.
在△ABE和△CAF中,{∠E=∠AFC,∠BAE=∠ACF,AB=CA}
∴△ABE≌△CAF(AAS),
∴AE=CF,BE=AF.
∵EF=AF+AE,
∴EF=BE+CF.
10.(2025·黑龙江哈尔滨巴彦期末)如图,点 B,E,C,F 在一条直线上,AB= DE,AC= DF,BE= CF.
(1)如图(1),求证:∠A= ∠D;
(2)如图(2),∠A= 70°,∠B= 40°,FG 平分∠DFE 交 AC 于点 G,求∠CGF 的度数.

(1)如图(1),求证:∠A= ∠D;
(2)如图(2),∠A= 70°,∠B= 40°,FG 平分∠DFE 交 AC 于点 G,求∠CGF 的度数.

答案:
(1)
∵BE=CF,
∴BE+EC=CF+EC,即BC=EF.
在△ABC和△DEF中,{BC=EF,AB=DE,AC=DF}
∴△ABC≌△DEF(SSS),
∴∠A=∠D.
(2)在△ABC中,∠A=70°,∠B=40°,
∴∠ACB=180°-(∠A+∠B)=70°.
由
(1)可知:△ABC≌△DEF,
∴∠ACB=∠DFE=70°.
∵FG平分∠DFE交AC于点G,
∴∠CFG=$\frac{1}{2}$∠DFE=35°.
∵∠ACB是△CFG的一个外角,
∴∠ACB=∠CFG+∠CGF,
∴70°=35°+∠CGF,
∴∠CGF=35°.
(1)
∵BE=CF,
∴BE+EC=CF+EC,即BC=EF.
在△ABC和△DEF中,{BC=EF,AB=DE,AC=DF}
∴△ABC≌△DEF(SSS),
∴∠A=∠D.
(2)在△ABC中,∠A=70°,∠B=40°,
∴∠ACB=180°-(∠A+∠B)=70°.
由
(1)可知:△ABC≌△DEF,
∴∠ACB=∠DFE=70°.
∵FG平分∠DFE交AC于点G,
∴∠CFG=$\frac{1}{2}$∠DFE=35°.
∵∠ACB是△CFG的一个外角,
∴∠ACB=∠CFG+∠CGF,
∴70°=35°+∠CGF,
∴∠CGF=35°.