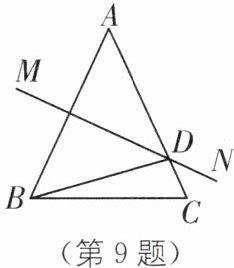
9. 如图,在△ABC 中,AB= AC= 14 cm,AB 的垂直平分线 MN 交 AC 于点 D,且△DBC 的周长是 24 cm,则 BC=
10
cm.
答案:10
解析:
∵MN是AB的垂直平分线,
∴AD=BD,
∵△DBC的周长是24 cm,
∴BD+DC+BC=24 cm,
∴AD+DC+BC=24 cm,即AC+BC=24 cm,
∵AC=14 cm,
∴BC=24-14=10 cm.
10
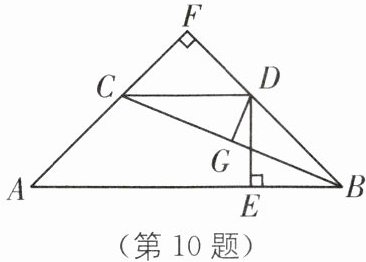
10.(2024·淮安清江浦区期中)如图,过△ABC 的边 BC 的垂直平分线 DG 上的点 D 作△ABC 另外两边 AB,AC 所在直线的垂线,垂足分别为 E,F,且 BE= CF. 求证:
(1)DF= DE;
(2)∠ACD+∠ABD= 180°.
]
(1)DF= DE;
(2)∠ACD+∠ABD= 180°.
]

答案:
(1)
∵D在BC的垂直平分线上,
∴CD=BD.
∵DE⊥AB,DF⊥AC,
∴∠DFC=90°,∠DEB=90°,
∴△CDF和△BDE为直角三角形.
在Rt△CDF和Rt△BDE中,$\left\{\begin{array}{l} CD=BD,\\ CF=BE,\end{array}\right. $
∴Rt△CDF≌Rt△BDE(HL),
∴DF=DE.
(2)
∵Rt△CDF≌Rt△BDE,
∴∠FCD=∠EBD.
∵∠FCD+∠ACD=180°,
∴∠ACD+∠ABD=180°.
(1)
∵D在BC的垂直平分线上,
∴CD=BD.
∵DE⊥AB,DF⊥AC,
∴∠DFC=90°,∠DEB=90°,
∴△CDF和△BDE为直角三角形.
在Rt△CDF和Rt△BDE中,$\left\{\begin{array}{l} CD=BD,\\ CF=BE,\end{array}\right. $
∴Rt△CDF≌Rt△BDE(HL),
∴DF=DE.
(2)
∵Rt△CDF≌Rt△BDE,
∴∠FCD=∠EBD.
∵∠FCD+∠ACD=180°,
∴∠ACD+∠ABD=180°.
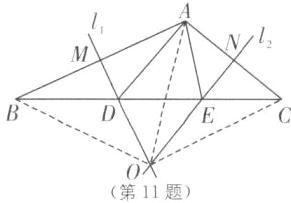
11.(2025·扬州江都区期中)如图,在△ABC 中,AB 的垂直平分线$ l_1 $交 AB 于点 M,交 BC 于点 D,AC 的垂直平分线$ l_2 $交 AC 于点 N,交 BC 于点$ E,l_1 $与$ l_2 $相交于点 O,△ADE 的周长为 12. 请你解答下列问题:
(1)求 BC 的长;
(2)试判断点 O 是否在边 BC 的垂直平分线上,并说明理由.
]

(1)求 BC 的长;
(2)试判断点 O 是否在边 BC 的垂直平分线上,并说明理由.
]

答案:
(1)
∵l₁垂直平分AB,
∴DB=DA,
同理可得EA=EC,
又△ADE的周长为12,
∴BC=BD+DE+EC=DA+DE+EA=12.
(2)点O在边BC的垂直平分线上,理由如下:
如图,连接AO,BO,CO,
∵l₁与l₂分别是AB,AC的垂直平分线,
∴AO=BO,CO=AO,
∴OB=OC,
∴点O在边BC的垂直平分线上.
(1)
∵l₁垂直平分AB,
∴DB=DA,
同理可得EA=EC,
又△ADE的周长为12,
∴BC=BD+DE+EC=DA+DE+EA=12.
(2)点O在边BC的垂直平分线上,理由如下:
如图,连接AO,BO,CO,
∵l₁与l₂分别是AB,AC的垂直平分线,
∴AO=BO,CO=AO,
∴OB=OC,
∴点O在边BC的垂直平分线上.

12. 将军饮马模型 新情境 修建水泵站选址 如图,要在河边修建一个水泵站,分别向张村 A 和李庄 B 送水. 水泵应建在什么地方,可使所用的水管最短?请在图中设计出水泵站的位置.
]

]

答案:
如图,作点A关于河边所在直线l的对称点A',连接A'B 交直线l于点P,则点P为水泵站的位置,此时PA+PB的长度之和最短,即所使用的水管最短.
PA+PB=PA'+PB=A'B,两点之间线段最短

如图,作点A关于河边所在直线l的对称点A',连接A'B 交直线l于点P,则点P为水泵站的位置,此时PA+PB的长度之和最短,即所使用的水管最短.
PA+PB=PA'+PB=A'B,两点之间线段最短

13.(2024·山东淄博周村区期中)如图,在△ABC 中,BC 边的垂直平分线交 AC 边于点 D,连接 BD.
(1)如图,若 CE= 4,△BDC 的周长为 18,求 BD 的长;
(2)若∠ADM= 60°,∠ABD= 20°,求∠A 的度数.
]

(1)如图,若 CE= 4,△BDC 的周长为 18,求 BD 的长;
(2)若∠ADM= 60°,∠ABD= 20°,求∠A 的度数.
]

答案:
(1)
∵MN垂直平分BC,
∴DC=BD,CE=EB.
又EC=4,
∴BE=4.又△BDC的周长=18,
∴BD+DC=18−2×4=10,
∴BD=5.
(2)
∵∠ADM=60°,
∴∠CDN=60°.
又MN垂直平分BC,
∴∠DEC=90°,
∴∠C=30°.
又∠C=∠DBC=30°,∠ABD=20°,
∴∠ABC=50°,
∴∠A=180°−∠C−∠ABC=100°.
归纳总结 本题考查了线段垂直平分线的性质,掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键.
(1)
∵MN垂直平分BC,
∴DC=BD,CE=EB.
又EC=4,
∴BE=4.又△BDC的周长=18,
∴BD+DC=18−2×4=10,
∴BD=5.
(2)
∵∠ADM=60°,
∴∠CDN=60°.
又MN垂直平分BC,
∴∠DEC=90°,
∴∠C=30°.
又∠C=∠DBC=30°,∠ABD=20°,
∴∠ABC=50°,
∴∠A=180°−∠C−∠ABC=100°.
归纳总结 本题考查了线段垂直平分线的性质,掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键.
14.(2024·凉山州中考)如图,在 Rt△ABC 中,∠ACB= 90°,DE 垂直平分 AB 交 BC 于点 D,若△ACD 的周长为 50 cm,则 AC+BC= (
A.25 cm
B.45 cm
C.50 cm
D.55 cm
]
C
).A.25 cm
B.45 cm
C.50 cm
D.55 cm
]
答案:C [解析]
∵DE垂直平分AB交BC于点D,
∴AD=DB.
∵△ACD的周长为50cm,
∴AC+AD+CD=AC+CD+DB=AC+BC=50cm 故选C;
∵DE垂直平分AB交BC于点D,
∴AD=DB.
∵△ACD的周长为50cm,
∴AC+AD+CD=AC+CD+DB=AC+BC=50cm 故选C;