1.(2025·扬州邗江区期末)在等腰三角形ABC中,∠A= 2∠B,则∠C的度数为______
45°或72°
.答案:45°或72° [解析]设∠B=x°,则∠A=2x°,当∠A是顶角时,∠A+2∠B=180°,即4x=180,解得x=45,此时∠C=∠B=45°;当∠A是底角时,2∠A+∠B=180°,即5x=180,解得x=36,此时∠C=2∠B=72°.故∠C的度数为45°或72°.
2. 中考新考法 新定义问题 (2025·镇江期中改编)若一个三角形的两个内角之差是第三个内角的一半,则称这个三角形是“差半角三角形”.若一个等腰三角形是“差半角三角形”,求它的底角度数.
答案:设等腰三角形的底角是α,则顶角是(180°-2α),其中α<90°,根据“差半角三角形”知当这个等腰三角形是“差半角三角形”时,有以下两种情况:①当(180°-2α)-α=α/2时,解得α=(360/7)°<90°,符合题意,②当α-(180°-2α)=α/2时,解得α=72°<90°,符合题意,综上所述,这个等腰三角形的底角度数是(360/7)°或72°.
解析:
设等腰三角形的底角是$\alpha$,则顶角是$(180^\circ - 2\alpha)$,其中$\alpha < 90^\circ$。
①当$(180^\circ - 2\alpha)-\alpha=\frac{\alpha}{2}$时,
$\begin{aligned}180^\circ - 3\alpha&=\frac{\alpha}{2}\\180^\circ&=\frac{7\alpha}{2}\\\alpha&=\frac{360^\circ}{7}\end{aligned}$
$\frac{360^\circ}{7} < 90^\circ$,符合题意。
②当$\alpha-(180^\circ - 2\alpha)=\frac{\alpha}{2}$时,
$\begin{aligned}3\alpha - 180^\circ&=\frac{\alpha}{2}\\frac{5\alpha}{2}&=180^\circ\\\alpha&=72^\circ\end{aligned}$
$72^\circ < 90^\circ$,符合题意。
综上所述,这个等腰三角形的底角度数是$\frac{360}{7}^\circ$或$72^\circ$。
①当$(180^\circ - 2\alpha)-\alpha=\frac{\alpha}{2}$时,
$\begin{aligned}180^\circ - 3\alpha&=\frac{\alpha}{2}\\180^\circ&=\frac{7\alpha}{2}\\\alpha&=\frac{360^\circ}{7}\end{aligned}$
$\frac{360^\circ}{7} < 90^\circ$,符合题意。
②当$\alpha-(180^\circ - 2\alpha)=\frac{\alpha}{2}$时,
$\begin{aligned}3\alpha - 180^\circ&=\frac{\alpha}{2}\\frac{5\alpha}{2}&=180^\circ\\\alpha&=72^\circ\end{aligned}$
$72^\circ < 90^\circ$,符合题意。
综上所述,这个等腰三角形的底角度数是$\frac{360}{7}^\circ$或$72^\circ$。
3. 等腰三角形的两边长分别为8和3,则第三边长为
8
.答案:8
解析:
当腰长为8时,三边长为8,8,3,满足三角形三边关系;当腰长为3时,三边长为3,3,8,因为$3+3=6\lt8$,不满足三角形三边关系,舍去。第三边长为8。
4. 中考新考法 新定义问题 (2025·扬州江都区期末)定义:一个三角形的一边长是另一边长的2倍,这样的三角形叫作“倍长三角形”.若等腰三角形ABC是“倍长三角形”,腰AB的长为6,则△ABC的周长为______
15
.答案:15 [解析]分两种情况:当等腰三角形的底边长BC是腰长AB的2倍时,
∵腰长AB=AC=6,
∴底边BC的长为12.
∵6+6=12,
∴不能组成三角形;当等腰三角形的腰长AB是底边长BC的2倍时,
∵腰长AB=AC=6,
∴底边BC的长为3,
∴△ABC的周长为6+6+3=15.综上所述,△ABC的周长为15.
∵腰长AB=AC=6,
∴底边BC的长为12.
∵6+6=12,
∴不能组成三角形;当等腰三角形的腰长AB是底边长BC的2倍时,
∵腰长AB=AC=6,
∴底边BC的长为3,
∴△ABC的周长为6+6+3=15.综上所述,△ABC的周长为15.
5.(2025·连云港赣榆区期中)如图,在等腰三角形ABC中,AB= AC,∠B= 50°,D为BC的中点,点E在AB上,∠AED= 69°,若点P是等腰三角形ABC的腰AC上的一点,则当△EDP为等腰三角形时,∠EDP的度数是______.
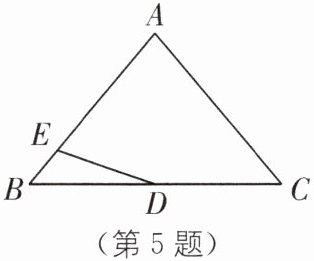

100°或142°
答案:100°或142° [解析]如图,连接AD,
∵AB=AC,∠B=50°,
∴∠BAC=180°-50°-50°=80°.
∵点P是等腰三角形ABC的腰AC上的一点,AB=AC,D为BC的中点,
∴∠BAD=∠CAD,过点D作DH⊥AC于点H,DG⊥AB于点G,
∴DG=DH.在Rt△DEG与Rt△DP₂H中,{DE=DP₂,{DG=DH,
∴Rt△DEG≌Rt△DP₂H(HL),
∴∠CP₂D=∠AED=69°,
∵∠BAC=80°,
∴∠EDP₂=100°,同理可得Rt△DEG≌Rt△DP₁H,
∴∠EDP₁=360°-69°-69°-80°=142°.
∵AB=AC,∠B=50°,
∴∠BAC=180°-50°-50°=80°.
∵点P是等腰三角形ABC的腰AC上的一点,AB=AC,D为BC的中点,
∴∠BAD=∠CAD,过点D作DH⊥AC于点H,DG⊥AB于点G,
∴DG=DH.在Rt△DEG与Rt△DP₂H中,{DE=DP₂,{DG=DH,
∴Rt△DEG≌Rt△DP₂H(HL),
∴∠CP₂D=∠AED=69°,
∵∠BAC=80°,
∴∠EDP₂=100°,同理可得Rt△DEG≌Rt△DP₁H,
∴∠EDP₁=360°-69°-69°-80°=142°.
6.(2025·南京秦淮区期中)如图,M,N是∠AOB的边OA上的两个点(OM<ON),∠AOB= 30°,OM= a,MN= 3,若边OB上有且只有1个点P,满足△PMN是等腰三角形,则a的取值范围是
a=3或a>6
.答案:a=3或a>6 [解析]①作线段MN的垂直平分线交OB于点P,连接PM,PN,如图所示:则PM=PN,此时△PMN是等腰三角形,过点M作MH⊥OB于点H,当MH>MN,满足条件的点P恰好只有一个.
∵MN=3,∠AOB=30°,当MH=3时,OM=2MH=6,
∴当a>6时,满足条件的点P恰好只有一个;②当△PMN是等边三角形时,满足条件的点P恰好只有一个,此时MN=MP,∠NMP=60°,
∵∠AOB=30°,
∴∠MPO=30°,
∴OM=MP=MN=3,
∴a=3.综上所述,满足条件的a的取值范围为a=3或a>6.
∵MN=3,∠AOB=30°,当MH=3时,OM=2MH=6,
∴当a>6时,满足条件的点P恰好只有一个;②当△PMN是等边三角形时,满足条件的点P恰好只有一个,此时MN=MP,∠NMP=60°,
∵∠AOB=30°,
∴∠MPO=30°,
∴OM=MP=MN=3,
∴a=3.综上所述,满足条件的a的取值范围为a=3或a>6.
7. 如图,∠AOB= 60°,C是BO延长线上一点,OC= 12 cm,动点M从点C出发沿射线CB以2 cm/s的速度移动,动点N从点O出发沿射线OA以1 cm/s的速度移动,如果点M,N同时出发,设运动的时间为t s,那么当t为何值时,△MON是等腰三角形?


答案:t的值为4或12. [解析]由题意知,当0<t≤6时,OM=12-2t;当t>6时,OM=2t-12,ON=t.
∵△MON是等腰三角形,
∴当0<t≤6时,OM=ON,即12-2t=t,解得t=4,当t>6时,△MON是等腰三角形,
∴OM=ON,即2t-12=t,解得t=12.综上所述,t的值为4或12.
∵△MON是等腰三角形,
∴当0<t≤6时,OM=ON,即12-2t=t,解得t=4,当t>6时,△MON是等腰三角形,
∴OM=ON,即2t-12=t,解得t=12.综上所述,t的值为4或12.