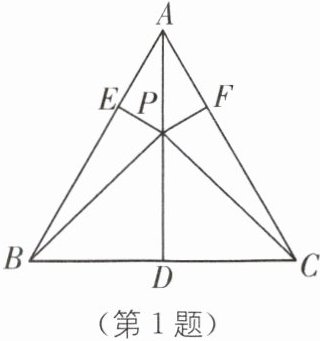
1. 如图,在△ABC中,AB= AC,D是边BC的中点,P是AD上任意一点,PE⊥AB于点E,PF⊥AC于点F.试说明:
(1)PE= PF;
(2)PB= PC.
(1)PE= PF;
(2)PB= PC.

答案:1.
(1)
∵AB=AC,D是边BC的中点,
∴AD平分∠BAC.又PE⊥AB于点E,PF⊥AC于点F,
∴PE=PF.
(2)
∵AB=AC,D是边BC的中点,
∴AD⊥BC,
∴AD垂直平分BC.
又P是AD上任意一点,
∴PB=PC.
方法诠释 解答本题需要应用到等腰三角形“三线合一”的性质、角平分线的性质及线段垂直平分线的性质.
(1)
∵AB=AC,D是边BC的中点,
∴AD平分∠BAC.又PE⊥AB于点E,PF⊥AC于点F,
∴PE=PF.
(2)
∵AB=AC,D是边BC的中点,
∴AD⊥BC,
∴AD垂直平分BC.
又P是AD上任意一点,
∴PB=PC.
方法诠释 解答本题需要应用到等腰三角形“三线合一”的性质、角平分线的性质及线段垂直平分线的性质.
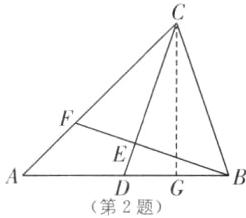
2.(2024·山东日照东港区期末)如图,在△ABC中,AC>BC,∠A= 45°,点D是AB边上一点,且CD= CB,过点B作BF⊥CD于点E,与AC交于点F.
(1)求证:$∠ABF= \frac{1}{2}∠BCD;$
(2)判断△BCF的形状,并说明理由.

(1)求证:$∠ABF= \frac{1}{2}∠BCD;$
(2)判断△BCF的形状,并说明理由.

答案:
2.
(1)如图,过点C作CG⊥AB于点G,
∴∠DCG+∠CDG=90°.
∵BC=DC,
∴∠BCG=∠DCG=$\frac{1}{2}$∠BCD.
∵BF⊥CD于点E,
∴∠ABF+∠CDG=90°,
∴∠ABF=∠DCG=$\frac{1}{2}$∠BCD.
(2)△BCF是等腰三角形.理由如下:
∵∠A=45°,CG⊥AB,
∴∠ACG=45°.
∵∠ACB=∠ACG+∠BCG,∠BFC=∠A+∠ABF,
∴∠ACB=45°+∠BCG,∠BFC=45°+∠ABF.
∵∠BCG=∠DCG=∠ABF,
∴∠BCF=∠BFC,
∴BC=BF,
∴△BCF是等腰三角形.
2.
(1)如图,过点C作CG⊥AB于点G,

∴∠DCG+∠CDG=90°.
∵BC=DC,
∴∠BCG=∠DCG=$\frac{1}{2}$∠BCD.
∵BF⊥CD于点E,
∴∠ABF+∠CDG=90°,
∴∠ABF=∠DCG=$\frac{1}{2}$∠BCD.
(2)△BCF是等腰三角形.理由如下:
∵∠A=45°,CG⊥AB,
∴∠ACG=45°.
∵∠ACB=∠ACG+∠BCG,∠BFC=∠A+∠ABF,
∴∠ACB=45°+∠BCG,∠BFC=45°+∠ABF.
∵∠BCG=∠DCG=∠ABF,
∴∠BCF=∠BFC,
∴BC=BF,
∴△BCF是等腰三角形.
3. 如图,在四边形ABCD中,AB//DC,AC平分∠DAB,CB⊥AB,CE⊥AD交AD的延长线于点E.
(1)求证:△ACD是等腰三角形;
(2)连接BE,求证:AC垂直平分BE.

(1)求证:△ACD是等腰三角形;
(2)连接BE,求证:AC垂直平分BE.

答案:3.
(1)
∵AB//DC,
∴∠DCA=∠CAB.
∵AC平分∠DAB,
∴∠DAC=∠CAB,
∴∠DCA=∠DAC,
∴DA=DC,
∴△ACD是等腰三角形.
(2)
∵AC是∠EAB的平分线,CE⊥AE,CB⊥AB,
∴CE=CB,∠CEA=∠CBA=90°.
又AC=AC,
∴Rt△CEA≌Rt△CBA(HL),
∴AE=AB,
∴点A,C在线段BE的垂直平分线上,
∴AC垂直平分BE.
(1)
∵AB//DC,
∴∠DCA=∠CAB.
∵AC平分∠DAB,
∴∠DAC=∠CAB,
∴∠DCA=∠DAC,
∴DA=DC,
∴△ACD是等腰三角形.
(2)
∵AC是∠EAB的平分线,CE⊥AE,CB⊥AB,
∴CE=CB,∠CEA=∠CBA=90°.
又AC=AC,
∴Rt△CEA≌Rt△CBA(HL),
∴AE=AB,
∴点A,C在线段BE的垂直平分线上,
∴AC垂直平分BE.
4.(2024·北京海淀外国语实验学校期中)在△ABC中,BE平分∠ABC,交AC边于点E.
(1)如图(1),过点E作DE//BC,交AB于点D,求证:△BDE为等腰三角形;
(2)如图(2),若AB= AC,AF⊥BD,$∠ACD= \frac{1}{2}∠ABC,$判断BF,CD,DF的数量关系,并说明理由.

(1)如图(1),过点E作DE//BC,交AB于点D,求证:△BDE为等腰三角形;
(2)如图(2),若AB= AC,AF⊥BD,$∠ACD= \frac{1}{2}∠ABC,$判断BF,CD,DF的数量关系,并说明理由.

答案:
4.
(1)
∵BE平分∠ABC,
∴∠ABE=∠EBC.
∵DE//BC,
∴∠DEB=∠EBC=∠ABE,
∴BD=ED,
∴△DBE为等腰三角形.
(2)BF=CD+DF.理由如下:如图,延长CD到点M,使得CM=BD,连接AM,过点A作AN⊥CM于点N.

∵BE平分∠ABC,∠ACD=$\frac{1}{2}$∠ABC,
∴∠ACM=∠ABD.
在△ABD和△ACM中,$\left\{\begin{array}{l} AB=AC,\\ ∠ABD=∠ACM,\\ BD=CM,\end{array}\right. $
∴△ABD≌△ACM(SAS),
∴AD=AM,∠ADB=∠AMC,
∴∠AMD=∠ADM,
∴∠ADF=∠ADN.
∵AN⊥DM,
∴DN=MN.
在△ADF和△ADN中,$\left\{\begin{array}{l} ∠AFD=∠AND=90^{\circ },\\ ∠ADF=∠ADN,\\ AD=AD,\end{array}\right. $
∴△ADF≌△ADN(AAS),
∴DF=DN=MN.
∵BD=CM,
∴BF=BD-DF=CM-MN=CN=CD+DN=CD+DF,即BF=CD+DF.
4.
(1)
∵BE平分∠ABC,
∴∠ABE=∠EBC.
∵DE//BC,
∴∠DEB=∠EBC=∠ABE,
∴BD=ED,
∴△DBE为等腰三角形.
(2)BF=CD+DF.理由如下:如图,延长CD到点M,使得CM=BD,连接AM,过点A作AN⊥CM于点N.

∵BE平分∠ABC,∠ACD=$\frac{1}{2}$∠ABC,
∴∠ACM=∠ABD.
在△ABD和△ACM中,$\left\{\begin{array}{l} AB=AC,\\ ∠ABD=∠ACM,\\ BD=CM,\end{array}\right. $
∴△ABD≌△ACM(SAS),
∴AD=AM,∠ADB=∠AMC,
∴∠AMD=∠ADM,
∴∠ADF=∠ADN.
∵AN⊥DM,
∴DN=MN.
在△ADF和△ADN中,$\left\{\begin{array}{l} ∠AFD=∠AND=90^{\circ },\\ ∠ADF=∠ADN,\\ AD=AD,\end{array}\right. $
∴△ADF≌△ADN(AAS),
∴DF=DN=MN.
∵BD=CM,
∴BF=BD-DF=CM-MN=CN=CD+DN=CD+DF,即BF=CD+DF.