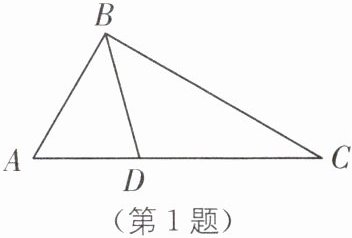
1. 如图,在$\triangle ABC$中,$\angle BAC = 2\angle C$,$BD为\triangle ABC$的角平分线,$BC = 5$,$AB = 3$,求$AD$的长.

答案:
如图,在BC上截取BE=AB,则CE=BC−BE=5−3=2.
∵BD为∠ABC的平分线,
∴∠ABD=∠CBD.
在△ABD和△EBD中,{AB=EB,∠ABD=∠EBD,BD=BD}
∴△ABD≌△EBD(SAS),
∴AD=DE、∠BED=∠A.
∵∠BAC=2∠C,∠BED=∠C+∠CDE,
∴∠C=∠CDE,
∴CE=DE=2,
∴AD=DE=2.

如图,在BC上截取BE=AB,则CE=BC−BE=5−3=2.
∵BD为∠ABC的平分线,
∴∠ABD=∠CBD.
在△ABD和△EBD中,{AB=EB,∠ABD=∠EBD,BD=BD}
∴△ABD≌△EBD(SAS),
∴AD=DE、∠BED=∠A.
∵∠BAC=2∠C,∠BED=∠C+∠CDE,
∴∠C=∠CDE,
∴CE=DE=2,
∴AD=DE=2.

变式1.1 如图,在四边形$ABCD$中,$AC$,$BD相交于点E$,$E为BD$的中点,$\angle BAC = 2\angle ACD$,$AE = 1$,$AC = 3.5$,求$AB$的长.


答案:
如图,过点D作DF//AB交AC于点F,
∴∠BAC=∠DFE.
∵E为BD的中点,
∴BE=DE.
在△ABE与△FDE中,{∠BAE=∠DFE,∠AEB=∠FED,BE=DE}
∴△ABE≌△FDE(AAS),
∴AE=FE=1,AB=FD.
∵∠BAC=2∠ACD、∠BAC=∠DFE=∠FDC+∠ACD,
∴∠FDC=∠FCD,
∴FD=FC,
∴AB=FC.
∵FC=AC−AF=3.5−2=1.5,
∴AB=1.5.

如图,过点D作DF//AB交AC于点F,
∴∠BAC=∠DFE.
∵E为BD的中点,
∴BE=DE.
在△ABE与△FDE中,{∠BAE=∠DFE,∠AEB=∠FED,BE=DE}
∴△ABE≌△FDE(AAS),
∴AE=FE=1,AB=FD.
∵∠BAC=2∠ACD、∠BAC=∠DFE=∠FDC+∠ACD,
∴∠FDC=∠FCD,
∴FD=FC,
∴AB=FC.
∵FC=AC−AF=3.5−2=1.5,
∴AB=1.5.

变式1.2 如图,点$D在\triangle ABC$的内部,$AD$,$BD$,$CD分别平分\angle BAC$,$\angle ABC$,$\angle ACB$,且$AB + BD = AC$. 求证:$\angle ABC = 2\angle ACB$.


答案:
如图,在AC上截取AE,使AE=AB,连接DE.

∵AD,BD,CD分别平分∠BAC,∠ABC,∠ACB,
∴∠DAB=∠DAE、∠DBA=∠DBC,∠DCA=∠DCB.
∵AB+BD=AC,AE=AB,AE+CE=AC,
∴DB=CE.
在△ADB和△ADE中,{AB=AE,∠DAB=∠DAE,AD=AD}
∴△ADB≌△ADE(SAS),
∴BD=DE,∠ABD=∠AED,
∴DE=CE,
∴∠EDC=∠ECD,
∴∠AED=2∠ECD,
∴∠ABD=2∠ECD,
∴∠ABC=2∠ACB.
如图,在AC上截取AE,使AE=AB,连接DE.

∵AD,BD,CD分别平分∠BAC,∠ABC,∠ACB,
∴∠DAB=∠DAE、∠DBA=∠DBC,∠DCA=∠DCB.
∵AB+BD=AC,AE=AB,AE+CE=AC,
∴DB=CE.
在△ADB和△ADE中,{AB=AE,∠DAB=∠DAE,AD=AD}
∴△ADB≌△ADE(SAS),
∴BD=DE,∠ABD=∠AED,
∴DE=CE,
∴∠EDC=∠ECD,
∴∠AED=2∠ECD,
∴∠ABD=2∠ECD,
∴∠ABC=2∠ACB.
变式1.3 如图,在$\triangle ABC$中,$\angle ABC = 2\angle ACB$,点$D在边BC$上,$AB + BD = AC$,求证$AD平分\angle BAC$.


答案:
如图,延长AB至点G,使BG=BD,连接DG,
则∠BDG=∠AGD,
∴∠ABC=∠BDG+∠AGD=2∠AGD.
∵∠ABC=2∠ACB,
∴∠AGD=∠ACB.
∵AB+BD=AC,BG=BD,AB+BG=AG,
∴AG=AC,
∴∠AGC=∠ACG,
∴∠DGC=∠DCG,
∴DG=DC.
在△ADG和△ADC中,{AG=AC,DG=DC,AD=AD}
∴△ADG≌△ADC(SSS),
∴∠DAG=∠DAC,
即AD平分∠BAC.

如图,延长AB至点G,使BG=BD,连接DG,
则∠BDG=∠AGD,
∴∠ABC=∠BDG+∠AGD=2∠AGD.
∵∠ABC=2∠ACB,
∴∠AGD=∠ACB.
∵AB+BD=AC,BG=BD,AB+BG=AG,
∴AG=AC,
∴∠AGC=∠ACG,
∴∠DGC=∠DCG,
∴DG=DC.
在△ADG和△ADC中,{AG=AC,DG=DC,AD=AD}
∴△ADG≌△ADC(SSS),
∴∠DAG=∠DAC,
即AD平分∠BAC.

2. 如图,在$\triangle ABC$中,$\angle BAC = 90^\circ$,$AB = AC$,$AD$是高,$E是AB$上一点,连接$DE$,过点$D作DF \perp DE$,交$AC于点F$,连接$EF$,交$AD于点G$.
(1)若$AB = 6$,$AE = 2$,求线段$AF$的长;
(2)求证:$\angle AGF = \angle AED$.

(1)若$AB = 6$,$AE = 2$,求线段$AF$的长;
(2)求证:$\angle AGF = \angle AED$.

答案:
(1)
∵在△ABC中,∠BAC=90°,AB=AC,AD是高,
∴BD=CD=AD=$\frac{1}{2}$BC,∠B=∠C=45°,∠BAD=∠CAD=$\frac{1}{2}$∠BAC=45°.
∵DF⊥DE,
∴∠EDF=∠ADC=90°,
∴∠ADE=∠CDF.
在△ADE和△CDF中,{∠ADE=∠CDF,AD=CD,∠EAD=∠C}
∴△ADE≌△CDF(ASA),
∴AE=CF=2.
∵AC=AB=6,
∴AF=AC−CF=6−2=4.
(2)由
(1),得△ADE≌△CDF,
∴DE=DF.
∵∠EDF=90°,
∴△DEF是等腰直角三角形,
∴∠DEF=∠DFE=45°.
∵∠AGF=∠DAE+∠AEG=45°+∠AEG,∠AED=∠DEF+∠AEG=45°+∠AEG,
∴∠AGF=∠AED.
(1)
∵在△ABC中,∠BAC=90°,AB=AC,AD是高,
∴BD=CD=AD=$\frac{1}{2}$BC,∠B=∠C=45°,∠BAD=∠CAD=$\frac{1}{2}$∠BAC=45°.
∵DF⊥DE,
∴∠EDF=∠ADC=90°,
∴∠ADE=∠CDF.
在△ADE和△CDF中,{∠ADE=∠CDF,AD=CD,∠EAD=∠C}
∴△ADE≌△CDF(ASA),
∴AE=CF=2.
∵AC=AB=6,
∴AF=AC−CF=6−2=4.
(2)由
(1),得△ADE≌△CDF,
∴DE=DF.
∵∠EDF=90°,
∴△DEF是等腰直角三角形,
∴∠DEF=∠DFE=45°.
∵∠AGF=∠DAE+∠AEG=45°+∠AEG,∠AED=∠DEF+∠AEG=45°+∠AEG,
∴∠AGF=∠AED.