1.(2025·山东临沂期末)以下列各组线段长为边,能组成三角形的是(
A.1 cm,2 cm,4 cm
B.8 cm,6 cm,2 cm
C.12 cm,5 cm,8 cm
D.2 cm,3 cm,6 cm
C
).A.1 cm,2 cm,4 cm
B.8 cm,6 cm,2 cm
C.12 cm,5 cm,8 cm
D.2 cm,3 cm,6 cm
答案:C [解析]A.
∵1+2<4,
∴不能组成三角形.故本选项不符合题意;B.
∵2+6=8,
∴不能组成三角形.故本选项不符合题意;C.
∵5+8>12,
∴能组成三角形.故本选项符合题意;D.
∵2+3<6,
∴不能组成三角形.故本选项不符合题意.故选C.
∵1+2<4,
∴不能组成三角形.故本选项不符合题意;B.
∵2+6=8,
∴不能组成三角形.故本选项不符合题意;C.
∵5+8>12,
∴能组成三角形.故本选项符合题意;D.
∵2+3<6,
∴不能组成三角形.故本选项不符合题意.故选C.
2.(2024·湖北咸宁期末)老师布置了一份家庭作业:用三根小木棍首尾相连拼出一个三角形,三根小木棍的长度分别为5 cm,9 cm,10.5 cm,并且只能对10.5 cm的小木棍进行裁切(裁切后,参与拼接的小木棍的长度为整数),则同学们最多能拼出不同的三角形的个数为(
A.4
B.5
C.6
D.7
C
).A.4
B.5
C.6
D.7
答案:C [解析]设从10.5cm的小木棍上裁切的木棍长度为xcm,则9−5<x<9+5且x<10.5,即4<x<10.5,
∴整数x的值为5,6,7,8,9,10,
∴同学们最多能拼出6个不同的三角形.故选C.
∴整数x的值为5,6,7,8,9,10,
∴同学们最多能拼出6个不同的三角形.故选C.
3.(2025·吉林四平期末)在学习了三角形后,老师给同学们每人准备了一根12 cm长的木棒,让同学们通过剪拼的形式,制作一个三角形木框.
(1)小明想把木棒剪成三段,第一段长a cm,第二段的长比第一段的3倍少2 cm.试判断第一段的长能否为3 cm,并说明理由;
(2)小亮先把木棒剪成如图所示的AB= 4 cm和CD= 8 cm的两段,现要将木棒CD从P处剪开,使得三根木棒首尾顺次相接能组成三角形,请直接写出符合条件的CP的整数长度.
]
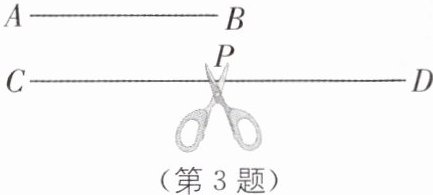
(1)小明想把木棒剪成三段,第一段长a cm,第二段的长比第一段的3倍少2 cm.试判断第一段的长能否为3 cm,并说明理由;
(2)小亮先把木棒剪成如图所示的AB= 4 cm和CD= 8 cm的两段,现要将木棒CD从P处剪开,使得三根木棒首尾顺次相接能组成三角形,请直接写出符合条件的CP的整数长度.
]

答案:
(1)第一段的长不能为3cm.理由如下:根据题意,得第一段长为acm,第二段的长为(3a−2)cm,第三段的长为[12−a−(3a−2)]=(14−4a)cm,当a=3cm时,3a−2=7cm,14−4a=2cm,
∵3+2<7,
∴三个木棒不能制作一个三角形木框,
∴第一段的长不能为3cm.
(2)设CP=xcm,则PD=(8−x)cm,
∵AB,CP,PD能组成三角形,
∴x+4>8−x且4+8−x>x,解得2<x<6,
∴整数x为3或4或5,即符合条件的CP的整数长度为3cm或4cm或5cm.
(1)第一段的长不能为3cm.理由如下:根据题意,得第一段长为acm,第二段的长为(3a−2)cm,第三段的长为[12−a−(3a−2)]=(14−4a)cm,当a=3cm时,3a−2=7cm,14−4a=2cm,
∵3+2<7,
∴三个木棒不能制作一个三角形木框,
∴第一段的长不能为3cm.
(2)设CP=xcm,则PD=(8−x)cm,
∵AB,CP,PD能组成三角形,
∴x+4>8−x且4+8−x>x,解得2<x<6,
∴整数x为3或4或5,即符合条件的CP的整数长度为3cm或4cm或5cm.
4. 一个三角形的周长为10 cm,其中两边长分别是x cm,(2x - 1) cm,则x的取值范围是
2<x<3
.答案:2<x<3 [解析]由题意,得{x+2x - 1>10 - (x+2x - 1),x+[10 - (x+2x - 1)]>2x - 1,2x - 1+[10 - (x+2x - 1)]>x,解得2<x<3.
解析:
由题意,得
$\begin{cases}x + (2x - 1) > 10 - (x + 2x - 1) \\x + [10 - (x + 2x - 1)] > 2x - 1 \\(2x - 1) + [10 - (x + 2x - 1)] > x\end{cases}$
解得$2 < x < 3$。
$2 < x < 3$
$\begin{cases}x + (2x - 1) > 10 - (x + 2x - 1) \\x + [10 - (x + 2x - 1)] > 2x - 1 \\(2x - 1) + [10 - (x + 2x - 1)] > x\end{cases}$
解得$2 < x < 3$。
$2 < x < 3$
5. 已知a,b,c是△ABC的三边长,若b= 2a - 1,c= a + 5,且△ABC的周长不超过20,求a的取值范围.
答案:由题意,得a+5+a+2a - 1≤20,解得a≤4,则a+5>2a - 1,故a+5<2a - 1+a,解得a>3.
∴a的取值范围为3<a≤4.
∴a的取值范围为3<a≤4.
6.(2025·河北保定期中)已知△ABC的三边长是a,b,c.
(1)用“>”或“<”填空:a - b + c
(2)化简:$|a - b + c| - |c - a - b| + |b + c - a|$.
(1)用“>”或“<”填空:a - b + c
>
0,c - a - b <
0,b + c - a >
0; (2)化简:$|a - b + c| - |c - a - b| + |b + c - a|$.
-a - b + 3c
答案:
(1)> < > [解析]
∵△ABC的三边长是a,b,c,
∴a+c>b,c - a<b,b+c>a,
∴a - b+c>0,c - a - b<0,b+c - a>0.
(2)由(1)可得,a - b+c>0,c - a - b<0,b+c - a>0,
∴原式=a - b+c+(c - a - b)+b+c - a =a - b+c+c - a - b+b+c - a = - a - b+3c.
(1)> < > [解析]
∵△ABC的三边长是a,b,c,
∴a+c>b,c - a<b,b+c>a,
∴a - b+c>0,c - a - b<0,b+c - a>0.
(2)由(1)可得,a - b+c>0,c - a - b<0,b+c - a>0,
∴原式=a - b+c+(c - a - b)+b+c - a =a - b+c+c - a - b+b+c - a = - a - b+3c.