7. 已知a,b,c为三角形的三边长,则b + a + c
>
2a(填“>”“<”或“=”).答案:>
解析:
∵a,b,c为三角形的三边长,
∴b + c > a,
∴b + a + c > a + a,
即b + a + c > 2a。
>
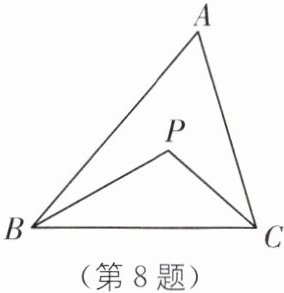
8. 如图,P为△ABC内任意一点,求证:AB + AC > PB + PC.
]
]

答案:
如图,延长BP交AC于点D,在△ABD中,PB+PD<AB+AD①,在△PCD中,PC<PD+CD②,由①+②,得PB+PD+PC<AB+AD+PD+CD,即PB+PC<AB+AC,即AB+AC>PB+PC.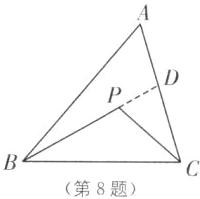
如图,延长BP交AC于点D,在△ABD中,PB+PD<AB+AD①,在△PCD中,PC<PD+CD②,由①+②,得PB+PD+PC<AB+AD+PD+CD,即PB+PC<AB+AC,即AB+AC>PB+PC.

9. 已知线段AB= 8 cm,BC= 3 cm.
(1)线段AC的长度 ______ 确定.(填“能”或“不能”)
(2)是否存在使A,C之间的距离最短的情形?若存在,求出此时AC的长度;若不存在,说明理由.
(3)能比较AB + BC与AC的大小吗?为什么?
(1)线段AC的长度 ______ 确定.(填“能”或“不能”)
不能
(2)是否存在使A,C之间的距离最短的情形?若存在,求出此时AC的长度;若不存在,说明理由.
存在使A,C之间的距离最短的情形,此时AC=AB - BC=8 - 3=5(cm).
(3)能比较AB + BC与AC的大小吗?为什么?
能.理由如下:①当点C在线段AB的延长线上时,AB+BC=AC;②当点C在线段AB上时,AB+BC>AC;③当点C在直线AB外时,AB+BC>AC,因为三角形两边之和大于第三边.综上所述,AB+BC≥AC.故能比较AB+BC与AC的大小.
答案:
(1)不能
(2)存在使A,C之间的距离最短的情形,此时AC=AB - BC=8 - 3=5(cm).
(3)能.理由如下:①当点C在线段AB的延长线上时,AB+BC=AC;②当点C在线段AB上时,AB+BC>AC;③当点C在直线AB外时,AB+BC>AC,因为三角形两边之和大于第三边.综上所述,AB+BC≥AC.故能比较AB+BC与AC的大小.
(1)不能
(2)存在使A,C之间的距离最短的情形,此时AC=AB - BC=8 - 3=5(cm).
(3)能.理由如下:①当点C在线段AB的延长线上时,AB+BC=AC;②当点C在线段AB上时,AB+BC>AC;③当点C在直线AB外时,AB+BC>AC,因为三角形两边之和大于第三边.综上所述,AB+BC≥AC.故能比较AB+BC与AC的大小.
10. 中考新考法 类比探究 观察并探索下列各问题,写出你通过观察得到的结论.
(1)如图(1),在△ABC中,P为边BC上一点,则BP + PC ______ AB + AC;(填“>”“<”或“=”)
(2)如图(2),试观察比较四边形$BP_1P_2C$的周长与△ABC的周长的大小,并说明理由.
]

(1)如图(1),在△ABC中,P为边BC上一点,则BP + PC ______ AB + AC;(填“>”“<”或“=”)
(2)如图(2),试观察比较四边形$BP_1P_2C$的周长与△ABC的周长的大小,并说明理由.
]

答案:
(1)<
(2)四边形BP₁P₂C的周长<△ABC的周长.理由如下:如图,分别延长BP₁,CP₂交于点M,易知,BM+CM<AB+AC.又P₁P₂<P₁M+P₂M,所以BP₁+P₁P₂+P₂C<BM+CM<AB+AC,所以四边形BP₁P₂C的周长<△ABC的周长.
(1)<

(2)四边形BP₁P₂C的周长<△ABC的周长.理由如下:如图,分别延长BP₁,CP₂交于点M,易知,BM+CM<AB+AC.又P₁P₂<P₁M+P₂M,所以BP₁+P₁P₂+P₂C<BM+CM<AB+AC,所以四边形BP₁P₂C的周长<△ABC的周长.