1. 如图,在五边形 $ABCDE$ 中,$AB = AE$,$BC = ED$,$\angle B= \angle E$,$AF\perp CD$ 于点 $F$.求证:
(1)$CF = FD$;
(2)$AF$ 平分 $\angle BAE$.
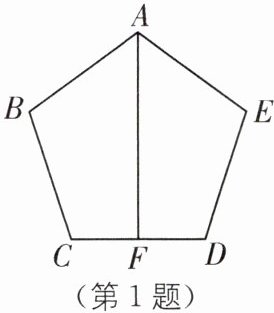
(1)$CF = FD$;
(2)$AF$ 平分 $\angle BAE$.

答案:1.
(1)连接AC,AD.
∵AB=AE,BC=ED,∠B=∠E,
∴△ABC≌△AED(SAS),
∴AC=AD,
又AF⊥CD,
∴CF=FD.
(2)
∵△ABC≌△AED,
∴∠BAC=∠EAD.
∵AC=AD,AF⊥CD,
∴∠CAF=∠DAF,
∴∠BAC+∠CAF=∠EAD+∠DAF,
∴∠BAF=∠EAF,
∴AF平分∠BAE.
(1)连接AC,AD.
∵AB=AE,BC=ED,∠B=∠E,
∴△ABC≌△AED(SAS),
∴AC=AD,
又AF⊥CD,
∴CF=FD.
(2)
∵△ABC≌△AED,
∴∠BAC=∠EAD.
∵AC=AD,AF⊥CD,
∴∠CAF=∠DAF,
∴∠BAC+∠CAF=∠EAD+∠DAF,
∴∠BAF=∠EAF,
∴AF平分∠BAE.
2. 如图,在 $\triangle ABC$ 中,$AB$ 的垂直平分线 $EF$ 交 $BC$ 于点 $E$,交 $AB$ 于点 $F$,$D$ 为线段 $CE$ 的中点,$BE = AC$.
(1)求证:$AD\perp BC$;
(2)若 $\angle BAC= 75^{\circ}$,求 $\angle B$ 的度数.

(1)求证:$AD\perp BC$;
(2)若 $\angle BAC= 75^{\circ}$,求 $\angle B$ 的度数.

答案:2.
(1)连接AE.
∵EF垂直平分AB,
∴AE=BE.
∵BE=AC,
∴AE=AC.
∵D是EC的中点,
∴AD⊥BC.
(2)设∠B=x°.
∵AE=BE,
∴∠BAE=∠B=x°.由三角形外角的性质,得∠AEC=2x°.
∵AE=AC,
∴∠C=∠AEC=2x°.
在△ABC中,3x°+75°=180°,解得x°=35°,
∴∠B=35°.
(1)连接AE.
∵EF垂直平分AB,
∴AE=BE.
∵BE=AC,
∴AE=AC.
∵D是EC的中点,
∴AD⊥BC.
(2)设∠B=x°.
∵AE=BE,
∴∠BAE=∠B=x°.由三角形外角的性质,得∠AEC=2x°.
∵AE=AC,
∴∠C=∠AEC=2x°.
在△ABC中,3x°+75°=180°,解得x°=35°,
∴∠B=35°.
3. 如图,在四边形 $ABCD$ 中,连接 $AC$,$BD$,$\angle ABD= \angle ACD = 60^{\circ}$,$\angle ADB= 90^{\circ}-\frac{1}{2}\angle BDC$.求证:$\triangle ABC$ 是等腰三角形.


答案:
3.如图,延长CD到点E,使DE=DB,连接AE.
∵∠ADB=90°-$\frac{1}{2}$∠BDC,
∴2∠ADB=180°-∠BDC=∠BDE,
∴∠1=∠2.
又DE=DB,AD=AD,
∴△ABD≌△AED(SAS),

∴∠ABD=∠E=60°,AB=AE.
∵∠ACD=60°,
∴∠CAE=60°=∠ACE=∠E,
∴△ACE是等边三角形,
∴AC=AE,
∴AB=AC,
∴△ABC是等腰三角形.
3.如图,延长CD到点E,使DE=DB,连接AE.
∵∠ADB=90°-$\frac{1}{2}$∠BDC,
∴2∠ADB=180°-∠BDC=∠BDE,
∴∠1=∠2.
又DE=DB,AD=AD,
∴△ABD≌△AED(SAS),

∴∠ABD=∠E=60°,AB=AE.
∵∠ACD=60°,
∴∠CAE=60°=∠ACE=∠E,
∴△ACE是等边三角形,
∴AC=AE,
∴AB=AC,
∴△ABC是等腰三角形.
4. 如图,$\angle BAD = 120^{\circ}$,$BD= DC$,$AB + AD= AC$.求证:$AC$ 平分 $\angle BAD$.


答案:
4.如图,延长BA到点E,使AE=AD,连接DE.
∵AB+AD=AC,
∴BE=AB+AE=AB+AD=AC.
∵∠BAD=120°,
∴∠DAE=60°,
∴△ADE是等边三角形,
∴DE=AD,∠E=60°.
又BD=DC,
∴△BDE≌△CDA(SSS),
∴∠CAD=∠E=60°,
∴∠BAC=∠BAD−∠CAD=60°=∠CAD,
∴AC平分∠BAD.

4.如图,延长BA到点E,使AE=AD,连接DE.
∵AB+AD=AC,
∴BE=AB+AE=AB+AD=AC.
∵∠BAD=120°,
∴∠DAE=60°,
∴△ADE是等边三角形,
∴DE=AD,∠E=60°.
又BD=DC,
∴△BDE≌△CDA(SSS),
∴∠CAD=∠E=60°,
∴∠BAC=∠BAD−∠CAD=60°=∠CAD,
∴AC平分∠BAD.
