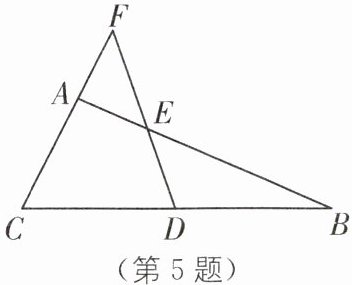
5. 如图,在 $\triangle ABC$ 中,过 $BC$ 的中点 $D$ 作直线交 $AB$ 于点 $E$,交 $CA$ 的延长线于点 $F$,且 $AE = AF$.求证:$BE= CF$.

答案:
5.如图,过点B作BG//CF交FD的延长线于点G,则∠G=∠F.
∵AE=AF,
∴∠F=∠AEF.
∵∠AEF=∠BEG,
∴∠G=∠BEG,
∴BE=BG.
∵∠BDG=∠CDF,∠G=∠F,BD=CD,
∴△GBD≌△FCD(AAS),
∴BG=CF,
∴BE=CF.
思路引导 解答本题时需要过点B作BG//CF交FD的延长线于点G,构造等腰三角形,然后再利用全等三角形和等腰三角形的性质和判定来解决问题

5.如图,过点B作BG//CF交FD的延长线于点G,则∠G=∠F.
∵AE=AF,
∴∠F=∠AEF.
∵∠AEF=∠BEG,
∴∠G=∠BEG,
∴BE=BG.
∵∠BDG=∠CDF,∠G=∠F,BD=CD,
∴△GBD≌△FCD(AAS),
∴BG=CF,
∴BE=CF.
思路引导 解答本题时需要过点B作BG//CF交FD的延长线于点G,构造等腰三角形,然后再利用全等三角形和等腰三角形的性质和判定来解决问题

6. 如图,在 $\triangle ABC$ 中,$AB = AC$,点 $E$ 在 $AC$ 上,点 $D$ 在 $BA$ 的延长线上,且 $AD = AE$,连接 $DE$.求证:$DE\perp BC$.


答案:6.过点E作EF//BC交AB于点F.
∵AB=AC,
∴∠B=∠C.
又EF//BC,
∴∠AFE=∠B,∠AEF=∠C,
∴∠AFE=∠AEF,
∵AD=AE,
∴∠D=∠AED.
在△DEF中,
∵∠D+∠AED+∠AEF+∠AFE=180°,
∴∠AED+∠AEF=180°×$\frac{1}{2}$=90°,
∴DE⊥EF.
∵EF//BC,
∴DE⊥BC.
∵AB=AC,
∴∠B=∠C.
又EF//BC,
∴∠AFE=∠B,∠AEF=∠C,
∴∠AFE=∠AEF,
∵AD=AE,
∴∠D=∠AED.
在△DEF中,
∵∠D+∠AED+∠AEF+∠AFE=180°,
∴∠AED+∠AEF=180°×$\frac{1}{2}$=90°,
∴DE⊥EF.
∵EF//BC,
∴DE⊥BC.
7. 如图,$AB$ 与 $CD$ 交于点 $E$,且 $AC = BD$,$\angle A+\angle B = 180^{\circ}$,求证:$CE= DE$.


答案:
7.如图,在线段AE上取点F,使AC=CF,
∴∠A=∠CFA.
∵∠A+∠B=180°,∠CFA+∠CFE=180°,
∴∠CFE=∠B.
∵AC=CF,AC=BD,
∴CF=DB.
在△CFE和△DBE中,
$\begin{cases} ∠CEF=∠DEB, \\ ∠CFE=∠B, \\ CF=DB, \end{cases}$
∴△CFE≌△DBE(AAS),
∴CE=DE.
解后反思 解答本题需要在线段AE上取点F,使AC=CF,然后利用等腰三角形的性质和判定以及全等三角形的判定和性质来进行证明.

7.如图,在线段AE上取点F,使AC=CF,
∴∠A=∠CFA.
∵∠A+∠B=180°,∠CFA+∠CFE=180°,
∴∠CFE=∠B.
∵AC=CF,AC=BD,
∴CF=DB.
在△CFE和△DBE中,
$\begin{cases} ∠CEF=∠DEB, \\ ∠CFE=∠B, \\ CF=DB, \end{cases}$
∴△CFE≌△DBE(AAS),
∴CE=DE.
解后反思 解答本题需要在线段AE上取点F,使AC=CF,然后利用等腰三角形的性质和判定以及全等三角形的判定和性质来进行证明.

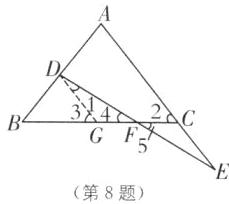
8. 如图,在 $\triangle ABC$ 中,$AB = AC$,$D$ 是 $AB$ 上一点,$E$ 是 $AC$ 延长线上一点,且 $CE= BD$,连接 $DE$ 交 $BC$ 于点 $F$.
(1)猜想 $DE$ 与 $EF$ 的大小关系;
(2)请证明你的猜想.

(1)猜想 $DE$ 与 $EF$ 的大小关系;
(2)请证明你的猜想.

答案:
8.
(1)DE=2EF.
(2)如图,过点D作DG//AE,交BC于点G,
则∠1=∠E,∠3=∠2.
∵AB=AC,
∴∠B=∠2,
∴∠B=∠3,
∴BD=DG.
∵CE=BD,
∴DG=CE.
在△DFG和△EFC中,
$\begin{cases} ∠4=∠5, \\ ∠1=∠E, \\ DG=EC, \end{cases}$
∴△DFG≌△EFC(AAS),
∴DF=EF,
∴DE=2EF.
方法诠释 解答本题时需要过点D作DG//AE,交BC 于点G,然后利用等腰三角形的性质和判定以及全等三角形的相关知识来解决问题.
8.
(1)DE=2EF.
(2)如图,过点D作DG//AE,交BC于点G,
则∠1=∠E,∠3=∠2.
∵AB=AC,
∴∠B=∠2,
∴∠B=∠3,
∴BD=DG.
∵CE=BD,
∴DG=CE.
在△DFG和△EFC中,
$\begin{cases} ∠4=∠5, \\ ∠1=∠E, \\ DG=EC, \end{cases}$
∴△DFG≌△EFC(AAS),
∴DF=EF,
∴DE=2EF.
方法诠释 解答本题时需要过点D作DG//AE,交BC 于点G,然后利用等腰三角形的性质和判定以及全等三角形的相关知识来解决问题.

9. 如图,在 $\triangle ABC$ 中,$\angle ACB= 2\angle B$,$BC = 2AC$,求证:$\angle A= 90^{\circ}$.


答案:
9.如图,作∠ACB的平分线CD 交AB于点D,过点D作DE⊥BC于点E.
∵∠ACB=2∠B,
∴∠B=∠BCD=$\frac{1}{2}$∠ACB,
∴BD=CD.
∵DE⊥BC,
∴BE=CE=$\frac{1}{2}$BC.
∵BC=2AC,
∴AC=CE.
在△ACD和△ECD中,
$\begin{cases} AC=EC, \\ ∠ACD=∠ECD, \\ CD=CD, \end{cases}$
∴△ACD≌△ECD(SAS),
∴∠A=∠CED=90°.
难点突破 由于题目中有两倍角关系,于是我们通过作角平分线来构造等腰三角形,然后再利用全等三角形和等腰三角形的性质和判定来进行证明

9.如图,作∠ACB的平分线CD 交AB于点D,过点D作DE⊥BC于点E.
∵∠ACB=2∠B,
∴∠B=∠BCD=$\frac{1}{2}$∠ACB,
∴BD=CD.
∵DE⊥BC,
∴BE=CE=$\frac{1}{2}$BC.
∵BC=2AC,
∴AC=CE.
在△ACD和△ECD中,
$\begin{cases} AC=EC, \\ ∠ACD=∠ECD, \\ CD=CD, \end{cases}$
∴△ACD≌△ECD(SAS),
∴∠A=∠CED=90°.
难点突破 由于题目中有两倍角关系,于是我们通过作角平分线来构造等腰三角形,然后再利用全等三角形和等腰三角形的性质和判定来进行证明
