1.(2024·南通海安期中)如图,在Rt△ABC中,∠ABC= 90°,AB= BC,D是AC上一点,AE⊥BD于点E,CF⊥BD于点F.
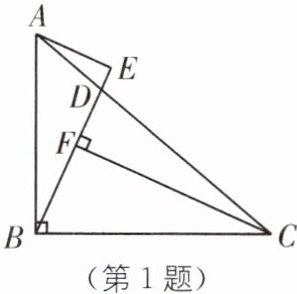
(1)求证:CF= BE;
(2)若BD= 2AE,求证:∠EAD= ∠ABE.

(1)求证:CF= BE;
(2)若BD= 2AE,求证:∠EAD= ∠ABE.
答案:1.
(1)
∵∠ABC=90°,CF⊥BD,AE⊥BD,
∴∠ABE+∠EBC=90°=∠EBC+∠BCF,
∴∠ABE=∠BCF.
又∠AEB=∠BFC=90°,AB=CB,
∴△ABE≌△BCF(AAS),
∴CF=BE.
(2)由
(1)△ABE≌△BCF,得BF=AE,∠ABE=∠BCF.
又BD=BF+FD=2AE,
∴BF=DF,
又CF⊥BD,
∴CB=CD,
∴CF平分∠ACB.
∵AE⊥BE,CF⊥BE,
∴AE//CF,
∴∠EAD=∠ACF.
∵∠ABE=∠BCF=∠ACF,
∴∠EAD=∠ABE.
归纳总结 本题考查全等三角形的判定和性质、线段的垂直平分线的性质、等腰三角形的性质等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.
(1)
∵∠ABC=90°,CF⊥BD,AE⊥BD,
∴∠ABE+∠EBC=90°=∠EBC+∠BCF,
∴∠ABE=∠BCF.
又∠AEB=∠BFC=90°,AB=CB,
∴△ABE≌△BCF(AAS),
∴CF=BE.
(2)由
(1)△ABE≌△BCF,得BF=AE,∠ABE=∠BCF.
又BD=BF+FD=2AE,
∴BF=DF,
又CF⊥BD,
∴CB=CD,
∴CF平分∠ACB.
∵AE⊥BE,CF⊥BE,
∴AE//CF,
∴∠EAD=∠ACF.
∵∠ABE=∠BCF=∠ACF,
∴∠EAD=∠ABE.
归纳总结 本题考查全等三角形的判定和性质、线段的垂直平分线的性质、等腰三角形的性质等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.
2.(2025·常州期末)如图,B是射线AD上一点(不与端点A重合),OP垂直平分线段AB,C是射线OP上一点(不与端点O重合),连接AC,BC.∠CBD的平分线与AC的延长线相交于点E.

(1)若∠A= 26°,求∠CBE的大小;
(2)若EC= EB,求∠A的大小.

(1)若∠A= 26°,求∠CBE的大小;
(2)若EC= EB,求∠A的大小.
答案:2.
(1)
∵OP垂直平分线段AB,
∴AC=BC,
∴∠A=∠CBA=26°,
∴∠CBD=154°.
∵BE平分∠CBD,
∴∠CBE=1/2∠CBD=77°.
(2)设∠A=∠CBA=x°,
∴∠ECB=(2x)°,
∵EC=EB,
∴∠CBE=∠ECB=(2x)°,
∴∠CBD=(4x)°,
∴5x=180,
解得x=36,
∴∠A=36°.
思路引导
(1)根据线段垂直平分线的性质得出AC=BC,进而利用等腰三角形的性质解答即可;
(2)根据等腰三角形的性质和平角的定义得出方程解答即可.
(1)
∵OP垂直平分线段AB,
∴AC=BC,
∴∠A=∠CBA=26°,
∴∠CBD=154°.
∵BE平分∠CBD,
∴∠CBE=1/2∠CBD=77°.
(2)设∠A=∠CBA=x°,
∴∠ECB=(2x)°,
∵EC=EB,
∴∠CBE=∠ECB=(2x)°,
∴∠CBD=(4x)°,
∴5x=180,
解得x=36,
∴∠A=36°.
思路引导
(1)根据线段垂直平分线的性质得出AC=BC,进而利用等腰三角形的性质解答即可;
(2)根据等腰三角形的性质和平角的定义得出方程解答即可.
3. 如图,在△ABC中,AB= AC,∠ABC,∠ACB的平分线交于点E,直线AE交BC于点D,求证:AD⊥BC.


答案:3.
∵AB=AC,
∴∠ABC=∠ACB.
∵BE平分∠ABC,CE平分∠ACB,
∴∠EBC=1/2∠ABC,∠ECB=1/2∠ACB,
∴∠EBC=∠ECB,
∴EB=EC.
又AB=AC,
∴AE垂直平分BC,
∴AD⊥BC.
∵AB=AC,
∴∠ABC=∠ACB.
∵BE平分∠ABC,CE平分∠ACB,
∴∠EBC=1/2∠ABC,∠ECB=1/2∠ACB,
∴∠EBC=∠ECB,
∴EB=EC.
又AB=AC,
∴AE垂直平分BC,
∴AD⊥BC.
4. 如图,在△ABC中,AB= AC,点D,E分别在CA,BA的延长线上,且BE= CD,连接BD,CE.
(1)求证:∠D= ∠E;
(2)若∠BAC= 108°,∠D= 36°,则图中共有

(1)求证:∠D= ∠E;
(2)若∠BAC= 108°,∠D= 36°,则图中共有
5
个等腰三角形.
答案:4.
(1)
∵AB=AC,
∴∠ABC=∠ACB.
在△EBC和△DCB中,{BE=CD,∠EBC=∠DCB,BC=CB,
∴△EBC≌△DCB(SAS),
∴∠D=∠E.
(2)5 [解析]
∵∠BAC=108°,AB=AC,
∴∠ABC=∠ACB=1/2×(180°-108°)=36°.
∵∠D=∠E=36°,
∴∠D=∠BCD,∠E=∠CBE,
∴BD=BC,BC=CE,∠DAB=∠EAC=72°,
∴∠DBA=∠DAB=72°,∠EAC=∠ECA=72°,
∴DB=DA,EA=EC,
∴△ABD,△AEC,△BCD,△BCE,△ABC是等腰三角形.故题图中共有5个等腰三角形.
(1)
∵AB=AC,
∴∠ABC=∠ACB.
在△EBC和△DCB中,{BE=CD,∠EBC=∠DCB,BC=CB,
∴△EBC≌△DCB(SAS),
∴∠D=∠E.
(2)5 [解析]
∵∠BAC=108°,AB=AC,
∴∠ABC=∠ACB=1/2×(180°-108°)=36°.
∵∠D=∠E=36°,
∴∠D=∠BCD,∠E=∠CBE,
∴BD=BC,BC=CE,∠DAB=∠EAC=72°,
∴∠DBA=∠DAB=72°,∠EAC=∠ECA=72°,
∴DB=DA,EA=EC,
∴△ABD,△AEC,△BCD,△BCE,△ABC是等腰三角形.故题图中共有5个等腰三角形.