5.(2024·淮安淮安区期中)如图,在△ABC中,CD⊥AB,垂足为D,BE⊥AC,垂足为E,连接DE,点G,F分别是BC,DE的中点.求证:GF⊥DE.
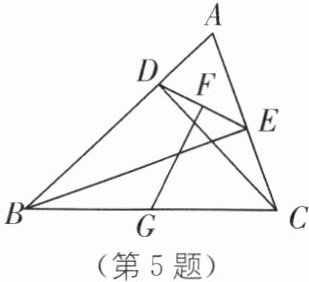

答案:5. 连接DG,EG.
∵CD⊥AB,点G是BC的中点,
∴在Rt△BCD中,DG=1/2BC.
同理,EG=1/2BC,
∴DG=EG.
又F是DE的中点,
∴GF⊥DE.
归纳总结 本题考查了直角三角形斜边上的中线、等腰三角形的判定与性质.熟练运用直角三角形斜边上的中线等于斜边的一半,是解题的关键.
∵CD⊥AB,点G是BC的中点,
∴在Rt△BCD中,DG=1/2BC.
同理,EG=1/2BC,
∴DG=EG.
又F是DE的中点,
∴GF⊥DE.
归纳总结 本题考查了直角三角形斜边上的中线、等腰三角形的判定与性质.熟练运用直角三角形斜边上的中线等于斜边的一半,是解题的关键.
6. 如图,点D,E在△ABC的边BC上,BD= AD= DE= AE= CE.
(1)求∠DAE的度数;
(2)求证:△ABC是等腰三角形.

(1)求∠DAE的度数;
(2)求证:△ABC是等腰三角形.

答案:6.
(1)
∵AD=DE=AE,
∴△ADE是等边三角形,
∴∠DAE=60°.
(2)
∵△ADE是等边三角形,
∴∠ADE=∠AED=60°.
∵BD=AD,
∴∠B=∠BAD.
∵∠ADE=∠B+∠BAD,
∴∠B=30°.
同理,∠C=30°,
∴∠B=∠C,
∴△ABC是等腰三角形.
(1)
∵AD=DE=AE,
∴△ADE是等边三角形,
∴∠DAE=60°.
(2)
∵△ADE是等边三角形,
∴∠ADE=∠AED=60°.
∵BD=AD,
∴∠B=∠BAD.
∵∠ADE=∠B+∠BAD,
∴∠B=30°.
同理,∠C=30°,
∴∠B=∠C,
∴△ABC是等腰三角形.
7.(2025·徐州邳州期中)如图,在△ABC中,AD⊥BC,E是AB的中点,DG垂直平分CE.
(1)求证:DC= BE;
(2)若∠B= 50°,求∠AEC的度数.

(1)求证:DC= BE;
(2)若∠B= 50°,求∠AEC的度数.

答案:7.
(1)
∵DG垂直平分CE,
∴DC=DE.
∵AD⊥BC,
∴∠ADB=90°.
∵E是AB的中点,
∴DE=1/2AB,
∴DE=BE,
∴DC=BE.
(2)由
(1)知DC=DE=BE,
∴∠BDE=∠B=50°,∠DCE=∠DEC.
∵∠BDE=∠DCE+∠DEC,
∴∠DCE=1/2∠BDE=25°,
∴∠AEC=∠B+∠DCE=50°+25°=75°.
(1)
∵DG垂直平分CE,
∴DC=DE.
∵AD⊥BC,
∴∠ADB=90°.
∵E是AB的中点,
∴DE=1/2AB,
∴DE=BE,
∴DC=BE.
(2)由
(1)知DC=DE=BE,
∴∠BDE=∠B=50°,∠DCE=∠DEC.
∵∠BDE=∠DCE+∠DEC,
∴∠DCE=1/2∠BDE=25°,
∴∠AEC=∠B+∠DCE=50°+25°=75°.
8.(2024·南通启东期中)如图,在△ABC中,AB= AC,∠BAC= 120°,AD⊥BC,垂足为G,且AD= AB,∠EDF= 60°,其两边分别交边AB,AC于点E,F.求证:
(1)△ABD是等边三角形;
(2)BE= AF.

(1)△ABD是等边三角形;
(2)BE= AF.

答案:8.
(1)
∵AB=AC,AD⊥BC,
∴∠BAD=∠DAC=1/2∠BAC.
∵∠BAC=120°,
∴∠BAD=∠DAC=1/2×120°=60°,
又AD=AB,
∴△ABD是等边三角形.
(2)
∵△ABD是等边三角形,
∴∠ABD=∠ADB=60°,BD=AD.
∵∠EDF=60°,
∴∠ADB=∠EDF,
∴∠ADB-∠ADE=∠EDF-∠ADE,
∴∠BDE=∠ADF.
在△BDE与△ADF中,{∠DBE=∠DAF=60°,BD=AD,∠BDE=∠ADF,
∴△BDE≌△ADF(ASA),
∴BE=AF.
思路引导 本题考查了等腰三角形的性质、全等三角形的判定与性质、等边三角形的判定与性质.熟练掌握等腰三角形的性质,并能进行推理论证是解决问题的关键.
(1)
∵AB=AC,AD⊥BC,
∴∠BAD=∠DAC=1/2∠BAC.
∵∠BAC=120°,
∴∠BAD=∠DAC=1/2×120°=60°,
又AD=AB,
∴△ABD是等边三角形.
(2)
∵△ABD是等边三角形,
∴∠ABD=∠ADB=60°,BD=AD.
∵∠EDF=60°,
∴∠ADB=∠EDF,
∴∠ADB-∠ADE=∠EDF-∠ADE,
∴∠BDE=∠ADF.
在△BDE与△ADF中,{∠DBE=∠DAF=60°,BD=AD,∠BDE=∠ADF,
∴△BDE≌△ADF(ASA),
∴BE=AF.
思路引导 本题考查了等腰三角形的性质、全等三角形的判定与性质、等边三角形的判定与性质.熟练掌握等腰三角形的性质,并能进行推理论证是解决问题的关键.