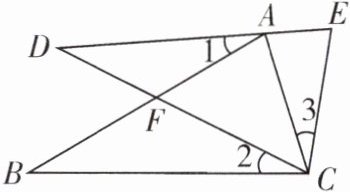
【例1】[全国初中数学竞赛(湖北武汉)预赛]如图,点A在DE上,点F在AB上,且AC= CE,∠1= ∠2= ∠3,则DE的长等于(
A.DC
B.BC
C.AB
D.AE+AC
C
).
A.DC
B.BC
C.AB
D.AE+AC
答案:解:
∵∠1+∠D=∠2+∠B,∠1=∠2,
∴∠D=∠B。
∵∠2=∠3,∠ACB=180°-∠2-∠ACF,∠ECD=180°-∠3-∠ACF,
∴∠ACB=∠ECD。
∵AC=CE,
∴△ABC≌△EDC(AAS)。
∴DE=AB。
答案:C
∵∠1+∠D=∠2+∠B,∠1=∠2,
∴∠D=∠B。
∵∠2=∠3,∠ACB=180°-∠2-∠ACF,∠ECD=180°-∠3-∠ACF,
∴∠ACB=∠ECD。
∵AC=CE,
∴△ABC≌△EDC(AAS)。
∴DE=AB。
答案:C
【例2】(第十七届江苏省初中数学竞赛)如图,在四边形ABCD中,对角线AC平分∠BAD,AB>AD,下列结论中正确的是(

A.AB-AD>CB-CD
B.AB-AD= CB-CD
C.AB-AD<CB-CD
D.AB-AD与CB-CD的大小关系不确定
A
). 
A.AB-AD>CB-CD
B.AB-AD= CB-CD
C.AB-AD<CB-CD
D.AB-AD与CB-CD的大小关系不确定
答案:解:在AB上截取AE=AD,连接EC。
∵AC平分∠BAD,
∴∠EAC=∠DAC。
在△AEC和△ADC中,
AE=AD,∠EAC=∠DAC,AC=AC,
∴△AEC≌△ADC(SAS),
∴EC=CD。
在△BEC中,BE>CB-EC(三角形两边之差小于第三边)。
∵BE=AB-AE=AB-AD,EC=CD,
∴AB-AD>CB-CD。
答案:A
∵AC平分∠BAD,
∴∠EAC=∠DAC。
在△AEC和△ADC中,
AE=AD,∠EAC=∠DAC,AC=AC,
∴△AEC≌△ADC(SAS),
∴EC=CD。
在△BEC中,BE>CB-EC(三角形两边之差小于第三边)。
∵BE=AB-AE=AB-AD,EC=CD,
∴AB-AD>CB-CD。
答案:A
1. (全国初中数学联赛)在$\triangle ABC$中,已知AC= 5,中线AD= 4,则边AB的取值范围是(
A.1<AB<9
B.3<AB<13
C.5<AB<13
D.9<AB<13
B
).A.1<AB<9
B.3<AB<13
C.5<AB<13
D.9<AB<13
答案:B[解析]延长 AD 到点 E,使 DE=AD,连接 EC,则△ABD≌△ECD,
∴AB=EC.
∵AD=4,
∴AE=AD+DE=8.在△ACE 中,AE - AC < CE < AE + AC,即 8 - 5 < CE < 8 + 5,
∴3 < CE < 13.
∴3 < AB < 13.故选 B.
∴AB=EC.
∵AD=4,
∴AE=AD+DE=8.在△ACE 中,AE - AC < CE < AE + AC,即 8 - 5 < CE < 8 + 5,
∴3 < CE < 13.
∴3 < AB < 13.故选 B.
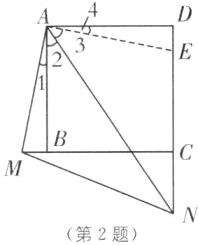
2. [全国初中数学竞赛(湖北荆州)预赛]在正方形ABCD中,$\angle MAN= 45^\circ,$$\angle MAN$绕点A顺时针旋转,它的两边分别交CB,DC(或它们的延长线)于点M,N.如果$\angle MAN$在如图(1)所示的位置时,有BM+DN= MN成立(不必证明).请问当$\angle MAN$绕点A旋转到如图(2)所示的位置时,线段BM,DN和MN之间又有怎样的数量关系?请说明理由.


答案:
DN - BM = MN.理由如下:
如图,在 DC 上截取 DE = BM,连接 AE.
在△ADE 和△ABM 中,
AD = AB,
∠D = ∠ABM,
DE = BM,
∴△ADE≌△ABM(SAS).
∴AE = AM,∠1 = ∠4.
∵∠1 + ∠2 = 45°,
∴∠2 + ∠4 = 45°,
∴∠3 = 45°,
∴∠MAN = ∠EAN.
在△AEN 和△AMN 中,
AE = AM,
∠EAN = ∠MAN,
AN = AN,
∴△AEN≌△AMN(SAS).
∴MN = EN,
∴MN = EN = DN - DE = DN - BM.
DN - BM = MN.理由如下:
如图,在 DC 上截取 DE = BM,连接 AE.

在△ADE 和△ABM 中,
AD = AB,
∠D = ∠ABM,
DE = BM,
∴△ADE≌△ABM(SAS).
∴AE = AM,∠1 = ∠4.
∵∠1 + ∠2 = 45°,
∴∠2 + ∠4 = 45°,
∴∠3 = 45°,
∴∠MAN = ∠EAN.
在△AEN 和△AMN 中,
AE = AM,
∠EAN = ∠MAN,
AN = AN,
∴△AEN≌△AMN(SAS).
∴MN = EN,
∴MN = EN = DN - DE = DN - BM.