15.(2023·重庆中考)计算:$|-5|+(2-\sqrt{3})^0= $
6
.答案：6 [解析]|-5|+(2 - √3)⁰ = 5 + 1 = 6.
解析：
$|-5|+(2-\sqrt{3})^0 = 5 + 1 = 6$
16.(2024·扬州邗江区期中)在计算器上依次按键：$\boxed{SHIFT}\ \boxed{\sqrt[3]{ }}\ \boxed{-}\ 8\ \boxed{-}\ \boxed{\sqrt{ }}\ 4\ \boxed{=}$,显示的结果为
-4
.答案：-4
解析：
$\sqrt[3]{-8}-\sqrt{4}=-2 - 2=-4$
17. 方程思想 中考新考法 新定义问题 如图,已知实数$a(a＞0)$在数轴上对应的位置为点 P. 现对点 P 进行如下操作:先把点 P 沿数轴以每秒 1 个单位的速度向左移动$t(t＞0)$秒,再把所得到的点沿数轴以每秒 2 个单位的速度向右移动$a$秒,得到点$P'$. 我们把这样的操作称为点 P 的“回移”,点$P'$为点 P 的“回移点”.
(1)当$t= 2$时,
①若$a= 4$,求点 P 的回移点$P'$表示的实数;
②若回移点$P'$与点 P 恰好重合,求$a$的值.
(2)是否存在这样的情况:原点 O,点 P 及其回移点$P'$中,一个点是以另外两点为端点的线段的三等分点？若存在,请用含$a的代数式表示t$;若不存在,请说明理由.
(1)当$t= 2$时,
①若$a= 4$,求点 P 的回移点$P'$表示的实数;
②若回移点$P'$与点 P 恰好重合,求$a$的值.
(2)是否存在这样的情况:原点 O,点 P 及其回移点$P'$中,一个点是以另外两点为端点的线段的三等分点？若存在,请用含$a的代数式表示t$;若不存在,请说明理由.
答案：
(1)①当 t = 2，a = 4 时，回移点 P'表示的实数是 4 - 2×1 + 2×4 = 10.②当 t = 2 时，回移点 P'表示的实数是 a - 2×1 + 2a = 3a - 2.
∵回移点 P'与点 P 恰好重合，
∴3a - 2 = a，解得 a = 1. 故 a 的值是 1.
(2)存在原点 O，点 P 及其回移点 P'中，一个点是以另外两点为端点的线段的三等分点. 理由如下:根据题意，得点 P 表示的数是 a，点 O 表示的数是 0，点 P'表示的数是 a - t + 2a = 3a - t，
∴OP = a，OP' = |3a - t|，PP' = |2a - t|.当 O 为 PP'的三等分点时，OP' = 2OP 或 OP' = 1/2OP，
∴|3a - t| = 2a 或|3a - t| = 1/2a，解得 t = a(不符合题意，舍去)或 t = 5a 或 t = 5/2a(不符合题意，舍去)或 t = 7/2a;当 P'是 OP 的三等分点时，OP' = 2PP'或 OP' = 1/2PP'，
∴|3a - t| = 2|2a - t|或|3a - t| = 1/2|2a - t|，解得 t = a(不符合题意，舍去)或 t = 7/3a 或 t = 4a(不符合题意，舍去)或 t = 8/3a;当 P 为 OP'的三等分点时，OP = 2PP'或 OP = 1/2PP'，
∴a = 2|2a - t|或 a = 1/2|2a - t|，解得 t = 3/2a 或 t = 5/2a(不符合题意，舍去)或 t = 4a(不符合题意，舍去)或 t = 0(不符合题意，舍去).综上所述，t = 5a 或 t = 7/2a 或 t = 7/3a 或 t = 8/3a 或 t = 3/2a.
(1)①当 t = 2，a = 4 时，回移点 P'表示的实数是 4 - 2×1 + 2×4 = 10.②当 t = 2 时，回移点 P'表示的实数是 a - 2×1 + 2a = 3a - 2.
∵回移点 P'与点 P 恰好重合，
∴3a - 2 = a，解得 a = 1. 故 a 的值是 1.
(2)存在原点 O，点 P 及其回移点 P'中，一个点是以另外两点为端点的线段的三等分点. 理由如下:根据题意，得点 P 表示的数是 a，点 O 表示的数是 0，点 P'表示的数是 a - t + 2a = 3a - t，
∴OP = a，OP' = |3a - t|，PP' = |2a - t|.当 O 为 PP'的三等分点时，OP' = 2OP 或 OP' = 1/2OP，
∴|3a - t| = 2a 或|3a - t| = 1/2a，解得 t = a(不符合题意，舍去)或 t = 5a 或 t = 5/2a(不符合题意，舍去)或 t = 7/2a;当 P'是 OP 的三等分点时，OP' = 2PP'或 OP' = 1/2PP'，
∴|3a - t| = 2|2a - t|或|3a - t| = 1/2|2a - t|，解得 t = a(不符合题意，舍去)或 t = 7/3a 或 t = 4a(不符合题意，舍去)或 t = 8/3a;当 P 为 OP'的三等分点时，OP = 2PP'或 OP = 1/2PP'，
∴a = 2|2a - t|或 a = 1/2|2a - t|，解得 t = 3/2a 或 t = 5/2a(不符合题意，舍去)或 t = 4a(不符合题意，舍去)或 t = 0(不符合题意，舍去).综上所述，t = 5a 或 t = 7/2a 或 t = 7/3a 或 t = 8/3a 或 t = 3/2a.
18. 数形结合思想 中考新考法 操作探究 数轴是一个非常重要的数学工具,它使数和数轴上的点建立起对应关系,揭示了数与点之间的内在联系,它是“数形结合”的基础. 小白在草稿纸上画了一条数轴进行操作探究：
操作一：
(1)折叠纸面,若使 1 表示的点与-1 表示的点重合,则-2 表示的点与______表示的点重合.
操作二：
(2)折叠纸面,若使 1 表示的点与-3 表示的点重合,回答以下问题：
①$\sqrt{3}$表示的点与数______表示的点重合；
②若数轴上 A,B 两点之间的距离为 8(A 在 B 的左侧),且 A,B 两点经折叠后重合,则 A,B 两点表示的数分别是______.
操作三：
(3)在数轴上剪下 9 个单位长度(从-1 到 8)的一条线段,并把这条线段沿某点折叠,然后在重叠部分某处剪一刀得到三条线段(如图). 若这三条线段的长度之比为 1∶1∶2,则折痕处对应的点所表示的数可能是多少?
]
操作一：
(1)折叠纸面,若使 1 表示的点与-1 表示的点重合,则-2 表示的点与______表示的点重合.
操作二：
(2)折叠纸面,若使 1 表示的点与-3 表示的点重合,回答以下问题：
①$\sqrt{3}$表示的点与数______表示的点重合；
②若数轴上 A,B 两点之间的距离为 8(A 在 B 的左侧),且 A,B 两点经折叠后重合,则 A,B 两点表示的数分别是______.
操作三：
(3)在数轴上剪下 9 个单位长度(从-1 到 8)的一条线段,并把这条线段沿某点折叠,然后在重叠部分某处剪一刀得到三条线段(如图). 若这三条线段的长度之比为 1∶1∶2,则折痕处对应的点所表示的数可能是多少?
]
答案：
(1)2 [解析]
∵1 表示的点与 - 1 表示的点重合，
∴折痕处对应的点为原点 O. 则 - 2 表示的点与 2 表示的点重合.
(2)① - 2 - √3 [解析]
∵折叠纸面，若使 1 表示的点与 - 3 表示的点重合，则折痕处对应的点所表示的数为 - 1.设√3表示的点与数 a 表示的点重合，则√3 - (-1) = - 1 - a，解得 a = - 2 - √3. ② - 5，3 [解析]
∵数轴上 A，B 两点之间的距离为 8，
∴数轴上 A，B 两点到折痕 - 1 的距离为 4.
∵A 在 B 的左侧，
∴A，B 两点表示的数分别是 - 5，3.
(3)设折痕处对应的点所表示的数是 x，如图
(1)，当 AB∶BC∶CD = 1∶1∶2 时，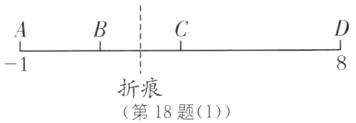
设 AB = a，BC = a，CD = 2a，则 a + a + 2a = 9，解得 a = 9/4，
∴AB = 9/4，BC = 9/4，CD = 9/2，
∴x = - 1 + 9/4 + 9/8 = 19/8;如图
(2)，当 AB∶BC∶CD = 1∶2∶1 时，
设 AB = a，BC = 2a，CD = a，则 a + a + 2a = 9，解得 a = 9/4，
∴AB = 9/4，BC = 9/2，CD = 9/4，
∴x = - 1 + 9/4 + 9/4 = 7/2;如图
(3)，当 AB∶BC∶CD = 2∶1∶1 时，
设 AB = 2a，BC = a，CD = a，则 a + a + 2a = 9，解得 a = 9/4，
∴AB = 9/2，BC = 9/4，CD = 9/4，
∴x = - 1 + 9/2 + 9/8 = 37/8.综上所述，折痕处对应的点所表示的数可能是 19/8 或 7/2 或 37/8. 名师点评 本题考查了实数和数轴的关系，及数轴上的折叠变换问题，明确①数轴上折叠后重合的点到折痕的距离相等;②数轴上任意两点的距离为两点坐标相减的绝对值. 本题第
(3)问注意需要用到分类讨论思想.
(1)2 [解析]
∵1 表示的点与 - 1 表示的点重合，
∴折痕处对应的点为原点 O. 则 - 2 表示的点与 2 表示的点重合.
(2)① - 2 - √3 [解析]
∵折叠纸面，若使 1 表示的点与 - 3 表示的点重合，则折痕处对应的点所表示的数为 - 1.设√3表示的点与数 a 表示的点重合，则√3 - (-1) = - 1 - a，解得 a = - 2 - √3. ② - 5，3 [解析]
∵数轴上 A，B 两点之间的距离为 8，
∴数轴上 A，B 两点到折痕 - 1 的距离为 4.
∵A 在 B 的左侧，
∴A，B 两点表示的数分别是 - 5，3.
(3)设折痕处对应的点所表示的数是 x，如图
(1)，当 AB∶BC∶CD = 1∶1∶2 时，
设 AB = a，BC = a，CD = 2a，则 a + a + 2a = 9，解得 a = 9/4，∴AB = 9/4，BC = 9/4，CD = 9/2，
∴x = - 1 + 9/4 + 9/8 = 19/8;如图
(2)，当 AB∶BC∶CD = 1∶2∶1 时，
设 AB = a，BC = 2a，CD = a，则 a + a + 2a = 9，解得 a = 9/4，∴AB = 9/4，BC = 9/2，CD = 9/4，
∴x = - 1 + 9/4 + 9/4 = 7/2;如图
(3)，当 AB∶BC∶CD = 2∶1∶1 时，
设 AB = 2a，BC = a，CD = a，则 a + a + 2a = 9，解得 a = 9/4，∴AB = 9/2，BC = 9/4，CD = 9/4，
∴x = - 1 + 9/2 + 9/8 = 37/8.综上所述，折痕处对应的点所表示的数可能是 19/8 或 7/2 或 37/8. 名师点评 本题考查了实数和数轴的关系，及数轴上的折叠变换问题，明确①数轴上折叠后重合的点到折痕的距离相等;②数轴上任意两点的距离为两点坐标相减的绝对值. 本题第
(3)问注意需要用到分类讨论思想.