6.(广东深圳中学自主招生)一个三角形三边长分别为5k,12k,13k,面积S≤900,满足情况的正整数k有
5
个.答案:6.5 [解析]由题意,得(5k)²+(12k)²=(13k)²,
∴三角形为直角三角形,且两直角边分别是5k,12k,
∴S=1/2×5k×12k=30k².
∵S≤900,
∴30k²≤900,
∴k²≤30.
又k为正整数,
∴k=1,2,3,4,5,
∴满足情况的正整数k有5个。
∴三角形为直角三角形,且两直角边分别是5k,12k,
∴S=1/2×5k×12k=30k².
∵S≤900,
∴30k²≤900,
∴k²≤30.
又k为正整数,
∴k=1,2,3,4,5,
∴满足情况的正整数k有5个。
7.中考新考法 课题实践活动 数学老师在一次“探究性学习”课中,设计了如下数表:
| n | 2 | 3 | 4 | 5 | ... |
| a | 3 | 8 | 15 | 24 | ... |
| b | 4 | 6 | 8 | 10 | ... |
| c | 5 | 10 | 17 | 26 | ... |
由表可知,当n= 2时,a= 3,b= 4,c= 5;当n= 3时,a= 8,b= 6,c= 10;….
(1)当n= 6时,a=
(2)请你分别观察a,b,c与n(n>1)之间的关系,并分别用含有n的代数式表示a,b,c:
a=
(3)猜想以a,b,c为边的三角形是否为直角三角形,并说明理由.
以a,b,c为边的三角形是直角三角形.理由如下:
∵a²+b²=(n²−1)²+4n²=n⁴+2n²+1,
c²=(n²+1)²=n⁴+2n²+1,
∴a²+b²=c²,
∴以a,b,c为边的三角形是直角三角形.
| n | 2 | 3 | 4 | 5 | ... |
| a | 3 | 8 | 15 | 24 | ... |
| b | 4 | 6 | 8 | 10 | ... |
| c | 5 | 10 | 17 | 26 | ... |
由表可知,当n= 2时,a= 3,b= 4,c= 5;当n= 3时,a= 8,b= 6,c= 10;….
(1)当n= 6时,a=
35
,b= 12
,c= 37
.(2)请你分别观察a,b,c与n(n>1)之间的关系,并分别用含有n的代数式表示a,b,c:
a=
n²−1
,b= 2n
,c= n²+1
.(3)猜想以a,b,c为边的三角形是否为直角三角形,并说明理由.
以a,b,c为边的三角形是直角三角形.理由如下:
∵a²+b²=(n²−1)²+4n²=n⁴+2n²+1,
c²=(n²+1)²=n⁴+2n²+1,
∴a²+b²=c²,
∴以a,b,c为边的三角形是直角三角形.
答案:7.
(1)35 12 37 [解析]
∵当n=2时,a=2²−1,b=2×2,c=2²+1;
当n=3时,a=3²−1,b=2×3,c=3²+1;
当n=4时,a=4²−1,b=2×4,c=4²+1;
当n=5时,a=5²−1,b=2×5,c=5²+1,
∴当n=6时,a=6²−1=35,b=2×6=12,c=6²+1 =37.
(2)n²−1 2n n²+1
(3)以a,b,c为边的三角形是直角三角形.理由如下:
∵a²+b²=(n²−1)²+4n²=n⁴+2n²+1,
c²=(n²+1)²=n⁴+2n²+1,
∴a²+b²=c²,
∴以a,b,c为边的三角形是直角三角形.
思路引导 本题考查了勾股定理的逆定理,解题的关键是仔细观察表中的数据,找出规律,进而利用勾股定理的逆定理解决问题。
(1)35 12 37 [解析]
∵当n=2时,a=2²−1,b=2×2,c=2²+1;
当n=3时,a=3²−1,b=2×3,c=3²+1;
当n=4时,a=4²−1,b=2×4,c=4²+1;
当n=5时,a=5²−1,b=2×5,c=5²+1,
∴当n=6时,a=6²−1=35,b=2×6=12,c=6²+1 =37.
(2)n²−1 2n n²+1
(3)以a,b,c为边的三角形是直角三角形.理由如下:
∵a²+b²=(n²−1)²+4n²=n⁴+2n²+1,
c²=(n²+1)²=n⁴+2n²+1,
∴a²+b²=c²,
∴以a,b,c为边的三角形是直角三角形.
思路引导 本题考查了勾股定理的逆定理,解题的关键是仔细观察表中的数据,找出规律,进而利用勾股定理的逆定理解决问题。
8.一题多问 传统文化 罗士琳法则 (2024·无锡江阴期中)如果直角三角形的三边的长都是正整数,这样的三个正整数叫作勾股数组.我国清代数学家罗士琳对勾股数组进行了深入研究,提出了各种有关公式400多个.他提出:当m,n为正整数,且m>n时$,m^2-n^2,2mn,m^2+n^2$为一组勾股数组,直到现在,人们都普遍采用他的这一公式.
(1)除勾股数3,4,5外,请再写出两组勾股数组
(2)若令$x= m^2-n^2,y= 2mn,z= m^2+n^2,$请你证明x,y,z为一组勾股数.
∵x=m²−n²,y=2mn,z=m²+n²,
∴x²=(m²−n²)²=m⁴+n⁴−2m²n²,y²=4m²n²,z²=(m²+n²)²=m⁴+n⁴+2m²n²,
∴x²+y²=(m⁴+n⁴−2m²n²)+4m²n²=m⁴+n⁴+2m²n²=z²,
∴x,y,z是一组勾股数。
(1)除勾股数3,4,5外,请再写出两组勾股数组
6,8,10
,5,12,13
;(2)若令$x= m^2-n^2,y= 2mn,z= m^2+n^2,$请你证明x,y,z为一组勾股数.
∵x=m²−n²,y=2mn,z=m²+n²,
∴x²=(m²−n²)²=m⁴+n⁴−2m²n²,y²=4m²n²,z²=(m²+n²)²=m⁴+n⁴+2m²n²,
∴x²+y²=(m⁴+n⁴−2m²n²)+4m²n²=m⁴+n⁴+2m²n²=z²,
∴x,y,z是一组勾股数。
答案:8.
(1)6,8,10 5,12,13(答案不唯一)
(2)
∵x=m²−n²,y=2mn,z=m²+n²,
∴x²=(m²−n²)²=m⁴+n⁴−2m²n²,y²=4m²n²,z²=(m²+n²)²=m⁴+n⁴+2m²n²,
∴x²+y²=(m⁴+n⁴−2m²n²)+4m²n²=m⁴+n⁴+2m²n²=z²,
∴x,y,z是一组勾股数。
(1)6,8,10 5,12,13(答案不唯一)
(2)
∵x=m²−n²,y=2mn,z=m²+n²,
∴x²=(m²−n²)²=m⁴+n⁴−2m²n²,y²=4m²n²,z²=(m²+n²)²=m⁴+n⁴+2m²n²,
∴x²+y²=(m⁴+n⁴−2m²n²)+4m²n²=m⁴+n⁴+2m²n²=z²,
∴x,y,z是一组勾股数。
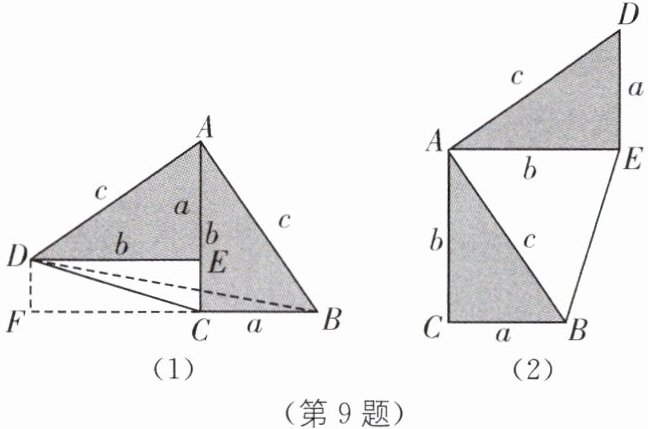
9.中考新考法 解题方法型阅读理解题 将两个全等的直角三角形按图(1)所示摆放,其中∠DAB= 90°,求证:a^2+b^2= c^2.
证明:连接DB,过点D作边BC上的高DF,则DF= EC= b-a.
∵S四边形ADCB= S△ACD+S△ABC= $\frac{1}{2}b^{2}+\frac{1}{2}ab$,
又S四边形ADCB= S△ADB+S△DCB= $\frac{1}{2}c^{2}+\frac{1}{2}a(b-a)$,
∴$\frac{1}{2}b^{2}+\frac{1}{2}ab= \frac{1}{2}c^{2}+\frac{1}{2}a(b-a)$,
∴$a^{2}+b^{2}= c^{2}$.
请参照上述证法,利用图(2)所示摆放,其中∠DAB= 90°.求证:$a^{2}+b^{2}= c^{2}$.
证明:连接DB,过点D作边BC上的高DF,则DF= EC= b-a.
∵S四边形ADCB= S△ACD+S△ABC= $\frac{1}{2}b^{2}+\frac{1}{2}ab$,
又S四边形ADCB= S△ADB+S△DCB= $\frac{1}{2}c^{2}+\frac{1}{2}a(b-a)$,
∴$\frac{1}{2}b^{2}+\frac{1}{2}ab= \frac{1}{2}c^{2}+\frac{1}{2}a(b-a)$,
∴$a^{2}+b^{2}= c^{2}$.
请参照上述证法,利用图(2)所示摆放,其中∠DAB= 90°.求证:$a^{2}+b^{2}= c^{2}$.

答案:
9.如图,连接BD,过点B作边DE上的高BF,则BF=b - a.
∵S五边形ACBED=S△ACB + S△ABE + S△ADE=1/2ab+1/2b²+1/2ab,S五边形ACBED=S△ACB + S△ABD + S△BDE=1/2ab+1/2c²+1/2a(b - a),

∴1/2ab+1/2b²+1/2ab=1/2ab+1/2c²+1/2a(b - a),
∴a²+b²=c².
归纳总结 本题考查了勾股定理的证明,用两种方法表示出五边形ACBED的面积是解本题的关键。
9.如图,连接BD,过点B作边DE上的高BF,则BF=b - a.
∵S五边形ACBED=S△ACB + S△ABE + S△ADE=1/2ab+1/2b²+1/2ab,S五边形ACBED=S△ACB + S△ABD + S△BDE=1/2ab+1/2c²+1/2a(b - a),

∴1/2ab+1/2b²+1/2ab=1/2ab+1/2c²+1/2a(b - a),
∴a²+b²=c².
归纳总结 本题考查了勾股定理的证明,用两种方法表示出五边形ACBED的面积是解本题的关键。