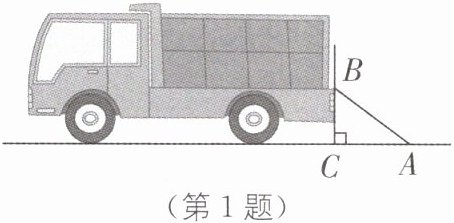
1. (教材 P101 习题 T1·变式)(2024·宿迁三模)有一辆装货的汽车,为了方便装运货物,使用了如图所示的钢架,其中∠ACB= 90°,AC= 1.2 m,BC= 0.9 m,则 AB 的长为(
A.1.2 m
B.1.5 m
C.1.8 m
D.15 m
B
).
A.1.2 m
B.1.5 m
C.1.8 m
D.15 m
答案:B [解析]
∵∠ACB=90°,AC=1.2 m,BC=0.9 m,
∴AB=√(BC²+AC²)=√(0.9²+1.2²)=1.5(m).
故选 B.
∵∠ACB=90°,AC=1.2 m,BC=0.9 m,
∴AB=√(BC²+AC²)=√(0.9²+1.2²)=1.5(m).
故选 B.
2. 新情境 实践探究活动 (2024·辽宁沈阳四十三中期中)某数学兴趣小组开展了笔记本电脑的张角大小的实践探究活动.如图,当张角为∠BAF时,顶部边缘 B 处离桌面的高度 BC 为 7 cm,此时底部边缘 A 处与 C 处间的距离 AC 为 24 cm,小组成员调整张角的大小继续探究,最后发现当张角为∠DAF时(点 D 是点 B 的对应点),顶部边缘 D 处到桌面的距离 DE 为 20 cm,则底部边缘 A 处与 E 之间的距离 AE 为(
A.15 cm
B.18 cm
C.21 cm
D.24 cm
A
).A.15 cm
B.18 cm
C.21 cm
D.24 cm
答案:A [解析] 由题意,得AC=24 cm,BC=7 cm,
在Rt△ABC中,AB=√(AC²+BC²)=25(cm).
∵AB=AD=25 cm,DE=20 cm,
∴在Rt△ADE中,AE=√(AD²-DE²)=√(25²-20²)
=15(cm). 故选 A.
在Rt△ABC中,AB=√(AC²+BC²)=25(cm).
∵AB=AD=25 cm,DE=20 cm,
∴在Rt△ADE中,AE=√(AD²-DE²)=√(25²-20²)
=15(cm). 故选 A.
3. (2025·连云港海州区期中)如图是一段楼梯,高 BC 是 5 米,斜边长 AB 是 13 米,如果在楼梯上铺地毯(不考虑台阶连接处损耗),那么地毯至少需要

17
米.
答案:17 [解析] △ABC是直角三角形,BC=5米,AB=13米,
由勾股定理得AC=√(AB²-BC²)=√(13²-5²)=12(米),
∴在楼梯上铺地毯至少需要地毯为AC+BC=12+5=
17(米).
归纳总结 本题考查了勾股定理的应用,把求地毯长转化为求两直角边长的和是解题的关键.
由勾股定理得AC=√(AB²-BC²)=√(13²-5²)=12(米),
∴在楼梯上铺地毯至少需要地毯为AC+BC=12+5=
17(米).
归纳总结 本题考查了勾股定理的应用,把求地毯长转化为求两直角边长的和是解题的关键.
4. 跨学科 光的反射 (2024·连云港期末)小丽在物理实验课上利用如图所示的“光的反射演示器”直观呈现了光的反射原理.她用激光笔从量角器左边边缘点 A 处发出光线,经量角器圆心 O 处(此处放置平面镜)反射后,反射光线落在右边光屏 CE 上的点 D 处(C 也在量角器的边缘上,O 为量角器的中心,C,O,B 三点共线,AB⊥BC,CE⊥BC).小丽在实验中还记录下了 AB= 6 cm,BC= 12 cm.依据记录的数据,求量角器的半径 OC 长.
 精题详解
精题详解
 精题详解
精题详解答案:
∵AB⊥BC,
∴∠ABC=90°.
设OA=OC=x cm,
∵BC=12 cm,
∴BO=BC-OC=(12-x)cm.
在Rt△ABO中,AB=6 cm,
∴AB²+OB²=OA²,
∴36+(12-x)²=x²,解得x=7.5,
∴OA=OC=7.5 cm,
∴量角器的半径OC长为7.5 cm.
∵AB⊥BC,
∴∠ABC=90°.
设OA=OC=x cm,
∵BC=12 cm,
∴BO=BC-OC=(12-x)cm.
在Rt△ABO中,AB=6 cm,
∴AB²+OB²=OA²,
∴36+(12-x)²=x²,解得x=7.5,
∴OA=OC=7.5 cm,
∴量角器的半径OC长为7.5 cm.
5. (2025·镇江期中)如图,将一根长 13 厘米的筷子置于底面直径为 6 厘米,高为 8 厘米的圆柱形杯子中,则筷子露在杯子外面的长度至少为(

A.1 厘米
B.2 厘米
C.3 厘米
D.4 厘米
C
).
A.1 厘米
B.2 厘米
C.3 厘米
D.4 厘米
答案:C
解析:
杯子底面直径为6厘米,则底面半径为3厘米,底面直径对应的弦长为6厘米。
杯子高为8厘米,筷子在杯中的最短长度为底面直径与高构成的直角三角形的斜边,根据勾股定理:
$\sqrt{6^2 + 8^2} = \sqrt{36 + 64} = \sqrt{100} = 10 厘米$
筷子总长13厘米,露在外面的长度至少为:
$13 - 10 = 3 厘米$
C
杯子高为8厘米,筷子在杯中的最短长度为底面直径与高构成的直角三角形的斜边,根据勾股定理:
$\sqrt{6^2 + 8^2} = \sqrt{36 + 64} = \sqrt{100} = 10 厘米$
筷子总长13厘米,露在外面的长度至少为:
$13 - 10 = 3 厘米$
C
6. 传统文化 《算法统宗》 在《算法统宗》中有一道“荡秋千”的问题:“平地秋千未起,踏板一尺离地.送行二步与人齐,五尺人高曾记.仕女佳人争蹴,终朝笑语欢嬉.良工高士素好奇,算出索长有几?”译文:“有一架秋千,当它静止时,踏板离地 1 尺,将它往前推送 10 尺(水平距离)时,秋千的踏板就和人一样高,这个人的身高为 5 尺,秋千的绳索始终拉得很直(如图所示),试问绳索有多长?”根据题意求出绳索的长为______尺.


14.5
答案:14.5 [解析] 设绳索的长为x尺,
则10²+(x+1-5)²=x²,解得x=14.5,
即绳索的长为14.5尺.
解后反思 在应用勾股定理解决实际问题时,勾股定理与方程的结合是解决实际问题常用的方法,关键是从题中抽象出勾股定理这一数学模型,画出准确的示意图,领会数形结合的思想的应用.
则10²+(x+1-5)²=x²,解得x=14.5,
即绳索的长为14.5尺.
解后反思 在应用勾股定理解决实际问题时,勾股定理与方程的结合是解决实际问题常用的方法,关键是从题中抽象出勾股定理这一数学模型,画出准确的示意图,领会数形结合的思想的应用.