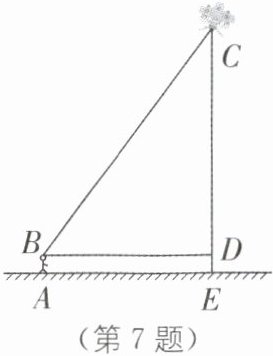
7. (2025·连云港海州区期中)“儿童散学归来早,忙趁东风放纸鸢”.又到了放风筝的最佳时节,某校八年级(1)班的小明和小亮学习了“勾股定理”之后,为了测得风筝的垂直高度 CE,他们进行了如下操作:①测得水平距离 BD 的长为 15 米;②根据手中剩余线的长度计算出风筝线 BC 的长为 25 米;③牵线放风筝的小明的身高为 1.6 米.求风筝的垂直高度 CE.

答案:由勾股定理,得CD²=BC²-BD²=25²-15²=400,
所以CD=20(负值舍去),
所以CE=CD+DE=20+1.6=21.6(米),
故风筝的高度CE为21.6米.
所以CD=20(负值舍去),
所以CE=CD+DE=20+1.6=21.6(米),
故风筝的高度CE为21.6米.
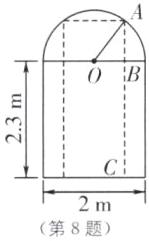
8. 一辆装满货物的卡车,高 2.5 m,宽 1.6 m,要开进形状如图所示的某工厂厂门,这辆卡车能否通过厂门? 说明你的理由.


答案:
这辆卡车能通过厂门.理由如下:
如图,由题意,得OA=2/2=1(m),
OB=1.6/2=0.8(m),
∴AB²=OA²-OB²=1²-0.8²=0.36,
∴AB=0.6 m,
∴AC=0.6+2.3=2.9(m).
∵2.5 m<2.9 m,
∴卡车能通过厂门.
这辆卡车能通过厂门.理由如下:
如图,由题意,得OA=2/2=1(m),
OB=1.6/2=0.8(m),

∴AB²=OA²-OB²=1²-0.8²=0.36,
∴AB=0.6 m,
∴AC=0.6+2.3=2.9(m).
∵2.5 m<2.9 m,
∴卡车能通过厂门.
9. 传统文化 《九章算术》 (2024·盐城盐都区期末)《九章算术》是我国古代数学名著.书中卷九“勾股”中记载:“今有垣高一丈,倚木于垣,上于垣齐.引木却行一尺,其木至地,问木长几何?”其意思是如图,墙 AB 高 1 丈(1 丈= 10 尺),一根木棒 AC 靠于墙上,木棒上端与墙头齐平.当木棒下端沿地面从 C 处向右滑 1 尺到 D 处时,木棒上端恰好沿墙壁从 A 处下滑到墙脚 B 处(∠ABC= 90°,B,C,D 在同一直线上),求木棒的长为多少尺.


答案:设木棒的长为x尺,则BC=(x-1)尺,
在Rt△ABC中,由勾股定理,得AB²+BC²=AC²,
∴10²+(x-1)²=x²,解得x=50.5.
故木棒的长为50.5尺.
在Rt△ABC中,由勾股定理,得AB²+BC²=AC²,
∴10²+(x-1)²=x²,解得x=50.5.
故木棒的长为50.5尺.
10. (2025·镇江句容期中)某条道路限速 80 km/h,如图,一辆小汽车在这条道路上沿直线行驶,某一时刻刚好行驶到路对面车速检测仪 A 处的正前方 30 m 的 C 处,过了 2 s,小汽车到达 B 处,此时测得小汽车与车速检测仪间的距离为 50 m.(1 m/s= 3.6 km/h)
(1)求 BC 的长.
(2)这辆小汽车超速了吗?

(1)求 BC 的长.
(2)这辆小汽车超速了吗?

答案:
(1)在Rt△ABC中,AC=30 m,AB=50 m,
由勾股定理可得BC=√(50²-30²)=40(m).
(2)
∵BC=40 m,
∴小汽车的速度为v=40/2=20(m/s)=20×3.6(km/h)=
72(km/h).
∵72 km/h<80 km/h,
∴这辆小汽车没有超速行驶.
(1)在Rt△ABC中,AC=30 m,AB=50 m,
由勾股定理可得BC=√(50²-30²)=40(m).
(2)
∵BC=40 m,
∴小汽车的速度为v=40/2=20(m/s)=20×3.6(km/h)=
72(km/h).
∵72 km/h<80 km/h,
∴这辆小汽车没有超速行驶.