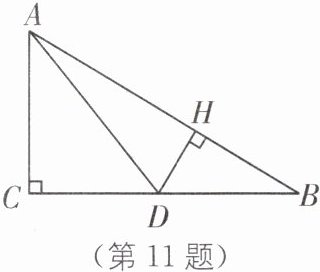
11. (2024·苏州平江中学期中)为推进乡村振兴,把家乡建设成为生态宜居、交通便利的美丽家园,某地大力修建崭新的公路.如图,现从 A 地分别向 C,D,B 三地修了三条笔直的公路 AC,AD 和 AB,C 地、D 地、B 地在同一直笔公路上,公路 AC 和公路 CB 互相垂直,又从 D 地修了一条笔直的公路 DH 与公路 AB 在 H 处连接,且公路 DH 和公路 AB 互相垂直,已知 AC= 9 千米,AB= 15 千米,BD= 5 千米.
(1)求公路 CD,AD 的长度;
(2)若修公路 DH 每千米的费用是 2000 万元,请求出修建公路 DH 的费用.
(1)求公路 CD,AD 的长度;
(2)若修公路 DH 每千米的费用是 2000 万元,请求出修建公路 DH 的费用.

答案:
(1)
∵∠C=90°,AC=9千米,AB=15千米,
∴BC=√(AB²-AC²)=12(千米).
∵BD=5千米,
∴CD=12-5=7(千米),
∴AD=√(AC²+CD²)=√130(千米).
(2)
∵DH⊥AB,
∴S△ABD=1/2BD·AC=1/2AB·DH,即5×9=15DH,
解得DH=3千米,
∴修建公路DH的费用为3×2000=6000(万元).
(1)
∵∠C=90°,AC=9千米,AB=15千米,
∴BC=√(AB²-AC²)=12(千米).
∵BD=5千米,
∴CD=12-5=7(千米),
∴AD=√(AC²+CD²)=√130(千米).
(2)
∵DH⊥AB,
∴S△ABD=1/2BD·AC=1/2AB·DH,即5×9=15DH,
解得DH=3千米,
∴修建公路DH的费用为3×2000=6000(万元).
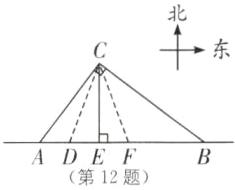
12. (2025·扬州江都区期中)台风是一种自然灾害,它在以台风中心为圆心,一定长度为半径的圆形区域内形成极端气候,有极强的破坏力.如图,监测中心监测到一台风中心沿监测点 B 与监测点 A 所在的直线由东向西移动,已知点 C 为一海港,且点 C 与 A,B 两点的距离分别为 300 km,400 km,且∠ACB= 90°,过点 C 作 CE⊥AB 于点 E,以台风中心为圆心,半径为 260 km 的圆形区域内为受影响区域.
(1)求监测点 A 与监测点 B 之间的距离;
(2)请判断海港 C 是否会受此次台风的影响,并说明理由;
(3)若台风的速度为 25 km/h,则台风影响该海港多长时间?

(1)求监测点 A 与监测点 B 之间的距离;
(2)请判断海港 C 是否会受此次台风的影响,并说明理由;
(3)若台风的速度为 25 km/h,则台风影响该海港多长时间?

答案:
(1)在Rt△ABC中,AC=300 km,BC=400 km,
∴AB=√(AC²+BC²)=√(300²+400²)=500(km).
故监测点A与监测点B之间的距离为500 km.
(2)海港C受台风影响,理由如下:
∵∠ACB=90°,CE⊥AB,
∴S△ABC=1/2AC·BC=1/2CE·AB,
∴300×400=500CE,
∴CE=240 km.
∵以台风中心为圆心周围260 km以内为受影响区域,
∴海港C会受到此次台风的影响.
(3)以C为圆心,260 km长为半径画弧,交AB于D,F,
则CD=CF=260 km,
在Rt△CDE中,
∵ED=√(CD²-CE²)=
√(260²-240²)=100(km),
∴DF=200 km.
∵台风的速度为25 km/h,
∴200÷25=8(h).
故台风影响该海港持续的时间为8 h.
(1)在Rt△ABC中,AC=300 km,BC=400 km,
∴AB=√(AC²+BC²)=√(300²+400²)=500(km).
故监测点A与监测点B之间的距离为500 km.
(2)海港C受台风影响,理由如下:
∵∠ACB=90°,CE⊥AB,
∴S△ABC=1/2AC·BC=1/2CE·AB,
∴300×400=500CE,
∴CE=240 km.
∵以台风中心为圆心周围260 km以内为受影响区域,
∴海港C会受到此次台风的影响.
(3)以C为圆心,260 km长为半径画弧,交AB于D,F,
则CD=CF=260 km,
在Rt△CDE中,
∵ED=√(CD²-CE²)=
√(260²-240²)=100(km),

∴DF=200 km.
∵台风的速度为25 km/h,
∴200÷25=8(h).
故台风影响该海港持续的时间为8 h.
13. 小伟准备用一段长 30 m 的篱笆围成一个三角形形状的小圈,用于饲养家兔.已知第一条边长为 a m,由于受地势限制,第二条边长只能是第一条边长的 2 倍多 2 m.
(1)请用 a 表示第三条边长.
(2)第一条边长可以为 7 m 吗? 为什么? 请说明理由,并求出 a 的取值范围.
(3)能否使得围成的小圈是直角三角形形状,且各边长均为整数? 若能,说出你的围法;若不能,请说明理由.
精题详解
(1)请用 a 表示第三条边长.
(2)第一条边长可以为 7 m 吗? 为什么? 请说明理由,并求出 a 的取值范围.
(3)能否使得围成的小圈是直角三角形形状,且各边长均为整数? 若能,说出你的围法;若不能,请说明理由.
精题详解
答案:
(1)由题意,得第二条边长为(2a+2)m,
∴第三条边长为30-a-(2a+2)=(28-3a)m.
(2)当a=7时,三边长分别为7 m,16 m,7 m.
∵7+7<16,
∴不能构成三角形,即第一条边长不能为7 m.
由{a+2a+2>28-3a, a+28-3a>2a+2}解得13/3<a<13/2,
即a的取值范围是13/3<a<13/2.
(3)在
(2)的条件下,a为整数时,a只能取5或6.
当a=5时,三角形的三边长分别为5 m,12 m,13 m.由5²+12²=13²知,恰好能构成直角三角形;当a=6时,三角形的三边长分别为6 m,14 m,10 m.由6²+10²≠14²知,此时不能构成直角三角形.
综上所述,能围成满足条件的小圈,它的三边长分别为5 m,12 m,13 m.
(1)由题意,得第二条边长为(2a+2)m,
∴第三条边长为30-a-(2a+2)=(28-3a)m.
(2)当a=7时,三边长分别为7 m,16 m,7 m.
∵7+7<16,
∴不能构成三角形,即第一条边长不能为7 m.
由{a+2a+2>28-3a, a+28-3a>2a+2}解得13/3<a<13/2,
即a的取值范围是13/3<a<13/2.
(3)在
(2)的条件下,a为整数时,a只能取5或6.
当a=5时,三角形的三边长分别为5 m,12 m,13 m.由5²+12²=13²知,恰好能构成直角三角形;当a=6时,三角形的三边长分别为6 m,14 m,10 m.由6²+10²≠14²知,此时不能构成直角三角形.
综上所述,能围成满足条件的小圈,它的三边长分别为5 m,12 m,13 m.