13. (2024·苏州吴江区二模)已知点$P(2a - 2,a + 5)$.
(1)若点$P在y$轴上,求出点$P$的坐标;
(2)若点$P$在第二象限,且它到$x$轴、$y$轴的距离相等,求$a^{2024} + 2024$的值.
(1)若点$P在y$轴上,求出点$P$的坐标;
(2)若点$P$在第二象限,且它到$x$轴、$y$轴的距离相等,求$a^{2024} + 2024$的值.
答案:
(1)
∵点P在y轴上,
∴$2a - 2 = 0$,解得$a = 1$,
∴$a + 5 = 6$,
∴$P(0,6)$。
(2)
∵点P到x轴和y轴距离相等,
∴$|2a - 2| = |a + 5|$。
∵点P在第二象限,
∴$2a - 2<0$,$a + 5>0$,
∴$|2a - 2| = 2 - 2a$,$|a + 5| = a + 5$,
∴$2 - 2a = a + 5$,
解得$a = - 1$,
∴$a^{2024}+2024 = (-1)^{2024}+2024 = 2025$。
(1)
∵点P在y轴上,
∴$2a - 2 = 0$,解得$a = 1$,
∴$a + 5 = 6$,
∴$P(0,6)$。
(2)
∵点P到x轴和y轴距离相等,
∴$|2a - 2| = |a + 5|$。
∵点P在第二象限,
∴$2a - 2<0$,$a + 5>0$,
∴$|2a - 2| = 2 - 2a$,$|a + 5| = a + 5$,
∴$2 - 2a = a + 5$,
解得$a = - 1$,
∴$a^{2024}+2024 = (-1)^{2024}+2024 = 2025$。
14. (教材 P118 习题 T3·变式)在平面直角坐标系中,点$A(-3,2)$,$B(3,5)$,$C(x,y)$,若$AC // x$轴,求线段$BC的最小值及此时点C$的坐标.
答案:
如图所示。
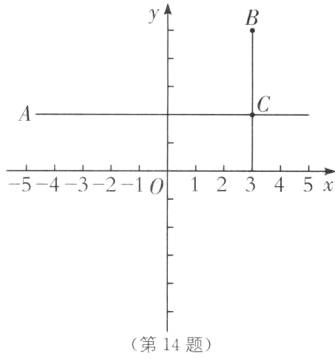
∵$AC// x$轴,$A(-3,2)$,
∴$y = 2$,
根据垂线段最短,当$BC⊥AC$于点C时,
点B到AC的距离最短,即BC的最小值$= 5 - 2 = 3$,
此时点C的坐标为$(3,2)$。
如图所示。

∵$AC// x$轴,$A(-3,2)$,
∴$y = 2$,
根据垂线段最短,当$BC⊥AC$于点C时,
点B到AC的距离最短,即BC的最小值$= 5 - 2 = 3$,
此时点C的坐标为$(3,2)$。
15. 分类讨论思想 中考新考法 新定义问题 [了解概念]
在平面直角坐标系xOy中,若P(a,b),Q(c,d),式子|a - c| + |b - d|的值就叫作线段PQ的“勾股距”,记作d_{PQ} = |a - c| + |b - d|,同时,我们把两边的“勾股距”之和等于第三边的“勾股距”的三角形叫作“等距三角形”. [理解运用] 在平面直角坐标系xOy中,A(2,3),B(4,2),C(m,n). (1)线段OA的“勾股距”d_{OA} =
在平面直角坐标系xOy中,若P(a,b),Q(c,d),式子|a - c| + |b - d|的值就叫作线段PQ的“勾股距”,记作d_{PQ} = |a - c| + |b - d|,同时,我们把两边的“勾股距”之和等于第三边的“勾股距”的三角形叫作“等距三角形”. [理解运用] 在平面直角坐标系xOy中,A(2,3),B(4,2),C(m,n). (1)线段OA的“勾股距”d_{OA} =
5
; (2)若点C在第三象限,且d_{OC} = 2d_{AB},求d_{AC}并判断$\triangle ABC$是否为“等距三角形”; [拓展提升] (3)若点C在x轴上$,\triangle ABC$是“等距三角形”,请直接写出m的取值范围.m≥4且m≠8
答案:
(1)5 [解析]由“勾股距”的定义知,
$d_{OA}=|0 - 2|+|0 - 3| = 2 + 3 = 5$。
(2)
∵$d_{AB}=|2 - 4|+|3 - 2| = 2 + 1 = 3$,
∴$d_{OC}=2d_{AB}=6$。
∵点C在第三象限,
∴$m<0$,$n<0$,$d_{OC}=|m - 0|+|n - 0| = |m|+|n| = - m - n = -(m + n)$,
∴$-(m + n)=6$,即$m + n = - 6$,
∴$d_{AC}=|2 - m|+|3 - n| = 2 - m + 3 - n = 5 - (m + n)=5 + 6 = 11$,$d_{BC}=|4 - m|+|2 - n| = 4 - m + 2 - n = 6 - (m + n)=6 + 6 = 12$。
∵$3 + 11≠12$,$11 + 12≠3$,$12 + 3≠11$,
∴$△ABC$不是“等距三角形”。
(3)当点C在x轴上时,设点$C(m,0)$,
则$d_{AC}=|2 - m|+3$,$d_{BC}=|4 - m|+2$。
①当$m<2$时,$d_{AC}=2 - m + 3 = 5 - m$,$d_{BC}=4 - m + 2 = 6 - m$。若$△ABC$是“等距三角形”,则$5 - m + 6 - m = 11 - 2m = 3$,解得$m = 4$(不合题意)。又$5 - m + 3 = 8 - m≠6 - m$,$6 - m + 3 = 9 - m≠5 - m$,
∴当$m<2$时,$△ABC$不是“等距三角形”;
②当$2≤m<4$时,$d_{AC}=m - 2 + 3 = m + 1$,$d_{BC}=4 - m + 2 = 6 - m$。若$△ABC$是“等距三角形”,则$m + 1 + 6 - m = 7≠3$(舍去),$6 - m + 3 = m + 1$,解得$m = 4$(不合题意),$m + 1 + 3 = 6 - m$,解得$m = 1$(不合题意),
∴当$2≤m<4$时,$△ABC$不是“等距三角形”;
③当$m≥4$时,$d_{AC}=m + 1$,$d_{BC}=m - 2$。若$△ABC$是“等距三角形”,则$m + 1 + m - 2 = 3$,解得$m = 2$(不合题意),$m + 1 + 3 = m + 4≠m - 2$(舍去),$m - 2 + 3 = m + 1$恒成立,
∴当$m≥4$时,$△ABC$是“等距三角形”。
当$m = 8$时,点A,B,C在同一直线上,无法构成三角形,
∴$m≠8$。
综上所述,当$△ABC$是“等距三角形”时,m的取值范围为$m≥4$且$m≠8$。
归纳总结 本题考查坐标与图形的性质,关键是对“勾股距”和“等距三角形”新概念的理解,运用“勾股距”和“等距三角形”解题。
(1)5 [解析]由“勾股距”的定义知,
$d_{OA}=|0 - 2|+|0 - 3| = 2 + 3 = 5$。
(2)
∵$d_{AB}=|2 - 4|+|3 - 2| = 2 + 1 = 3$,
∴$d_{OC}=2d_{AB}=6$。
∵点C在第三象限,
∴$m<0$,$n<0$,$d_{OC}=|m - 0|+|n - 0| = |m|+|n| = - m - n = -(m + n)$,
∴$-(m + n)=6$,即$m + n = - 6$,
∴$d_{AC}=|2 - m|+|3 - n| = 2 - m + 3 - n = 5 - (m + n)=5 + 6 = 11$,$d_{BC}=|4 - m|+|2 - n| = 4 - m + 2 - n = 6 - (m + n)=6 + 6 = 12$。
∵$3 + 11≠12$,$11 + 12≠3$,$12 + 3≠11$,
∴$△ABC$不是“等距三角形”。
(3)当点C在x轴上时,设点$C(m,0)$,
则$d_{AC}=|2 - m|+3$,$d_{BC}=|4 - m|+2$。
①当$m<2$时,$d_{AC}=2 - m + 3 = 5 - m$,$d_{BC}=4 - m + 2 = 6 - m$。若$△ABC$是“等距三角形”,则$5 - m + 6 - m = 11 - 2m = 3$,解得$m = 4$(不合题意)。又$5 - m + 3 = 8 - m≠6 - m$,$6 - m + 3 = 9 - m≠5 - m$,
∴当$m<2$时,$△ABC$不是“等距三角形”;
②当$2≤m<4$时,$d_{AC}=m - 2 + 3 = m + 1$,$d_{BC}=4 - m + 2 = 6 - m$。若$△ABC$是“等距三角形”,则$m + 1 + 6 - m = 7≠3$(舍去),$6 - m + 3 = m + 1$,解得$m = 4$(不合题意),$m + 1 + 3 = 6 - m$,解得$m = 1$(不合题意),
∴当$2≤m<4$时,$△ABC$不是“等距三角形”;
③当$m≥4$时,$d_{AC}=m + 1$,$d_{BC}=m - 2$。若$△ABC$是“等距三角形”,则$m + 1 + m - 2 = 3$,解得$m = 2$(不合题意),$m + 1 + 3 = m + 4≠m - 2$(舍去),$m - 2 + 3 = m + 1$恒成立,
∴当$m≥4$时,$△ABC$是“等距三角形”。
当$m = 8$时,点A,B,C在同一直线上,无法构成三角形,
∴$m≠8$。
综上所述,当$△ABC$是“等距三角形”时,m的取值范围为$m≥4$且$m≠8$。
归纳总结 本题考查坐标与图形的性质,关键是对“勾股距”和“等距三角形”新概念的理解,运用“勾股距”和“等距三角形”解题。