1. 实验班原创 如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(-1,1),第2次接着运动到点(-2,0),第3次接着运动到点(-3,2),…,按这样的运动规律,经过第2025次运动后,动点P的坐标是(
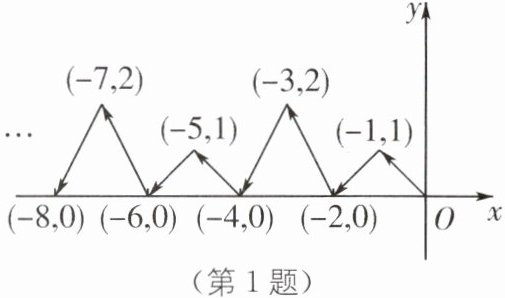
A.(2025,0)
B.(-2025,1)
C.(-2025,0)
D.(-2025,2)
B
).
A.(2025,0)
B.(-2025,1)
C.(-2025,0)
D.(-2025,2)
答案:B [解析]根据动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(-1,1),第2次接着运动到点(-2,0),第3次接着运动到点(-3,2),…,第4次运动到点(-4,0),第5次接着运动到点(-5,1),…,
∴横坐标为运动次数的相反数,
∴经过第2025次运动后,动点P的横坐标为-2025.
∵纵坐标为1,0,2,0,每4次一轮,2025÷4=506……1,
∴经过第2025次运动后,动点P的纵坐标为四个数中的第1个,即为1,
∴经过第2025次运动后,动点P的坐标是(-2025,1).故选B.
∴横坐标为运动次数的相反数,
∴经过第2025次运动后,动点P的横坐标为-2025.
∵纵坐标为1,0,2,0,每4次一轮,2025÷4=506……1,
∴经过第2025次运动后,动点P的纵坐标为四个数中的第1个,即为1,
∴经过第2025次运动后,动点P的坐标是(-2025,1).故选B.
2. (2024·甘南州中考)如图,在平面直角坐标系中,一动点从原点O出发,按向上,向右,向下,向右的方向不断地移动,每移动一个单位,得到点$A_1(0,1),A_2(1,1),A_3(1,0),A_4(2,0),…,$那么点$A_2₀_2₀$的坐标为______.


(1010,0)
答案:(1010,0) [解析]根据题意可知,A₁(0,1),A₂(1,1),A₃(1,0),A₄(2,0),A₅(2,1),A₆(3,1),A₇(3,0),A₈(4,0),…,可得坐标规律为A₄ₙ(2n,0),A₄ₙ₊₁(2n,1),A₄ₙ₊₂(2n+1,1),A₄ₙ₊₃(2n+1,0).
∵2020=4×505,
∴点A₂₀₂₀的坐标为(1010,0).
∵2020=4×505,
∴点A₂₀₂₀的坐标为(1010,0).
3. (2024·绥化中考)如图,在平面直角坐标系中,已知$A_1(1,-\sqrt{3}),$$A_2(3,-\sqrt{3}),$A_3(4,0),A_4(6,0),$A_5(7,\sqrt{3}),$$A_6(9,\sqrt{3}),$A_7(10,0),$A_8(11,-\sqrt{3}),$…,依此规律,则点A_2₀_2_4的坐标为______.


(2891,-√3)
答案:(2891,-√3) [解析]由题知,点A₁的坐标为(1,-√3),点A₂的坐标为(3,-√3),点A₃的坐标为(4,0),点A₄的坐标为(6,0),点A₅的坐标为(7,√3),点A₆的坐标为(9,√3),点A₇的坐标为(10,0),点A₈的坐标为(11,-√3),点A₉的坐标为(13,-√3),点A₁₀的坐标为(14,0),点A₁₁的坐标为(16,0),…,由此可见,每隔七个点,点Aₙ的横坐标增加10,且纵坐标按-√3,-√3,0,0,√3,√3,0循环出现,又因为2024÷7=289……1,所以1+289×10=2891,则点A₂₀₂₄的坐标为(2891,-√3).
解析:
由题知,点$A_1(1,-\sqrt{3})$,$A_2(3,-\sqrt{3})$,$A_3(4,0)$,$A_4(6,0)$,$A_5(7,\sqrt{3})$,$A_6(9,\sqrt{3})$,$A_7(10,0)$,$A_8(11,-\sqrt{3})$,$A_9(13,-\sqrt{3})$,$A_{10}(14,0)$,$A_{11}(16,0)$,…,
观察可得,每隔七个点,横坐标增加$10$,纵坐标按$-\sqrt{3},-\sqrt{3},0,0,\sqrt{3},\sqrt{3},0$循环出现。
$2024÷7=289\cdots\cdots1$,
横坐标:$1 + 289×10=2891$,
纵坐标:循环中第$1$个为$-\sqrt{3}$,
则点$A_{2024}$的坐标为$(2891,-\sqrt{3})$。
$(2891,-\sqrt{3})$
观察可得,每隔七个点,横坐标增加$10$,纵坐标按$-\sqrt{3},-\sqrt{3},0,0,\sqrt{3},\sqrt{3},0$循环出现。
$2024÷7=289\cdots\cdots1$,
横坐标:$1 + 289×10=2891$,
纵坐标:循环中第$1$个为$-\sqrt{3}$,
则点$A_{2024}$的坐标为$(2891,-\sqrt{3})$。
$(2891,-\sqrt{3})$
4. 在同一平面内,若一个点到一条直线的距离不大于1,则称这个点是该直线的“伴侣点”. 在平面直角坐标系中,已知点M(1,0),过点M作直线l平行于y轴,点A(-1,a),点B(b,2a),点$C(-\frac{1}{2},a-1),$将三角形ABC进行平移,平移后点A的对应点为点D,点B的对应点为点E,点C的对应点为点F.
(1)试判断点A是否是直线l的“伴侣点”?请说明理由.
(2)若点F刚好落在直线l上,F的纵坐标为a+b,点E落在x轴上,且△MFD的面积为$\frac{1}{12},$试判断点B是否是直线l的“伴侣点”?请说明理由.
精题详解
(1)试判断点A是否是直线l的“伴侣点”?请说明理由.
(2)若点F刚好落在直线l上,F的纵坐标为a+b,点E落在x轴上,且△MFD的面积为$\frac{1}{12},$试判断点B是否是直线l的“伴侣点”?请说明理由.
精题详解
答案:
(1)不是.理由如下:
∵点A的坐标为(-1,a),
∴点A到直线l的距离为2.又2>1,
∴点A不是直线l的“伴侣点”.
(2)点B是直线l的“伴侣点”.理由如下:
∵C(-1/2,a-1),F(1,a+b),
∴平移后的对应点横坐标增加了3/2,纵坐标增加了b+1,
∴D(1/2,a+b+1),E(b+3/2,2a+b+1).
∵点E落在x轴上,
∴2a+b+1=0.
∵△MFD的面积为1/12,
∴1/2×1/2|a+b|=1/12,
∴a+b=±1/3.当a+b=1/3时,解得a=-4/3,b=5/3,此时点B的坐标为(5/3,-8/3),点B是直线l的“伴侣点”;当a+b=-1/3时,解得a=-2/3,b=1/3,此时点B的坐标为(1/3,-4/3),点B是直线l的“伴侣点”.
(1)不是.理由如下:
∵点A的坐标为(-1,a),
∴点A到直线l的距离为2.又2>1,
∴点A不是直线l的“伴侣点”.
(2)点B是直线l的“伴侣点”.理由如下:
∵C(-1/2,a-1),F(1,a+b),
∴平移后的对应点横坐标增加了3/2,纵坐标增加了b+1,
∴D(1/2,a+b+1),E(b+3/2,2a+b+1).
∵点E落在x轴上,
∴2a+b+1=0.
∵△MFD的面积为1/12,
∴1/2×1/2|a+b|=1/12,
∴a+b=±1/3.当a+b=1/3时,解得a=-4/3,b=5/3,此时点B的坐标为(5/3,-8/3),点B是直线l的“伴侣点”;当a+b=-1/3时,解得a=-2/3,b=1/3,此时点B的坐标为(1/3,-4/3),点B是直线l的“伴侣点”.