【例】(江苏省初中数学竞赛)如图,在平面直角坐标系中,多边形ABCDEFGH是正八边形,点A的坐标为(1,0),点B的坐标为(0,1),则点E的坐标为
(1+√2,2+√2)
.答案:【解析】:
本题主要考查正八边形的性质以及平面直角坐标系中点的坐标确定。
1. 首先,根据正八边形的性质,我们知道正八边形的各边相等,各内角也相等。由于点$A$的坐标为$(1,0)$,点$B$的坐标为$(0,1)$,可以确定线段$AB$的长度为$\sqrt{(1-0)^2 + (0-1)^2} = \sqrt{2}$。
2. 接着,由于正八边形的对称性,我们可以知道点$E$的横坐标与点$H$的横坐标相等,点$E$的纵坐标与延长$ED$交$y$轴于点$M$的纵坐标相等。
3. 为了找到点$E$的坐标,我们需要先找到点$M$的坐标。由于$\angle DCM = 45^\circ$(正八边形的内角),在$Rt\triangle MCD$中,我们可以利用等腰直角三角形的性质来求解。
4. 已知$CD = \sqrt{2}$,由于$\angle DCM = 45^\circ$,则$MC = MD = 1$(等腰直角三角形的两直角边相等)。因此,$OM = OC + CM = 1 + 1 + \sqrt{2} × \frac{\sqrt{2}}{2} = 2 + \sqrt{2}$(这里$\sqrt{2} × \frac{\sqrt{2}}{2}$是$CD$在$y$轴上的投影长度)。
5. 所以,点$E$的坐标为$(1 + \sqrt{2}, 2 + \sqrt{2})$。
【答案】:
$(1 + \sqrt{2}, 2 + \sqrt{2})$
本题主要考查正八边形的性质以及平面直角坐标系中点的坐标确定。
1. 首先,根据正八边形的性质,我们知道正八边形的各边相等,各内角也相等。由于点$A$的坐标为$(1,0)$,点$B$的坐标为$(0,1)$,可以确定线段$AB$的长度为$\sqrt{(1-0)^2 + (0-1)^2} = \sqrt{2}$。
2. 接着,由于正八边形的对称性,我们可以知道点$E$的横坐标与点$H$的横坐标相等,点$E$的纵坐标与延长$ED$交$y$轴于点$M$的纵坐标相等。
3. 为了找到点$E$的坐标,我们需要先找到点$M$的坐标。由于$\angle DCM = 45^\circ$(正八边形的内角),在$Rt\triangle MCD$中,我们可以利用等腰直角三角形的性质来求解。
4. 已知$CD = \sqrt{2}$,由于$\angle DCM = 45^\circ$,则$MC = MD = 1$(等腰直角三角形的两直角边相等)。因此,$OM = OC + CM = 1 + 1 + \sqrt{2} × \frac{\sqrt{2}}{2} = 2 + \sqrt{2}$(这里$\sqrt{2} × \frac{\sqrt{2}}{2}$是$CD$在$y$轴上的投影长度)。
5. 所以,点$E$的坐标为$(1 + \sqrt{2}, 2 + \sqrt{2})$。
【答案】:
$(1 + \sqrt{2}, 2 + \sqrt{2})$
1.(全国初中数学竞赛)如图,在平面直角坐标系xOy中,等腰梯形ABCD的顶点坐标分别为A(1,1),B(2,-1),C(-2,-1),D(-1,1).将y轴上一点P(0,2)绕点A旋转180°得点P1,点P1绕点B旋转180°得点P2,点P2绕点C旋转180°得点P3,点P3绕点D旋转180°得点P4,…,重复操作依次得到点P1,P2,…,则点P2024的坐标是(
A.(2022,2)
B.(2022,-2)
C.(2024,2)
D.(0,2)
C
).A.(2022,2)
B.(2022,-2)
C.(2024,2)
D.(0,2)
答案:C
解析:
设点$P_n$的坐标为$(x_n,y_n)$。
已知$P(0,2)$,即$P_0(0,2)$。
求$P_1$:
点$P$绕点$A(1,1)$旋转$180^\circ$得$P_1$,则$A$是$PP_1$的中点。
$\frac{0+x_1}{2}=1$,解得$x_1=2$;$\frac{2+y_1}{2}=1$,解得$y_1=0$。
$\therefore P_1(2,0)$。
求$P_2$:
点$P_1$绕点$B(2,-1)$旋转$180^\circ$得$P_2$,则$B$是$P_1P_2$的中点。
$\frac{2+x_2}{2}=2$,解得$x_2=2$;$\frac{0+y_2}{2}=-1$,解得$y_2=-2$。
$\therefore P_2(2,-2)$。
求$P_3$:
点$P_2$绕点$C(-2,-1)$旋转$180^\circ$得$P_3$,则$C$是$P_2P_3$的中点。
$\frac{2+x_3}{2}=-2$,解得$x_3=-6$;$\frac{-2+y_3}{2}=-1$,解得$y_3=0$。
$\therefore P_3(-6,0)$。
求$P_4$:
点$P_3$绕点$D(-1,1)$旋转$180^\circ$得$P_4$,则$D$是$P_3P_4$的中点。
$\frac{-6+x_4}{2}=-1$,解得$x_4=4$;$\frac{0+y_4}{2}=1$,解得$y_4=2$。
$\therefore P_4(4,2)$。
求$P_5$:
点$P_4$绕点$A(1,1)$旋转$180^\circ$得$P_5$,则$A$是$P_4P_5$的中点。
$\frac{4+x_5}{2}=1$,解得$x_5=-2$;$\frac{2+y_5}{2}=1$,解得$y_5=0$。
$\therefore P_5(-2,0)$。
求$P_6$:
点$P_5$绕点$B(2,-1)$旋转$180^\circ$得$P_6$,则$B$是$P_5P_6$的中点。
$\frac{-2+x_6}{2}=2$,解得$x_6=6$;$\frac{0+y_6}{2}=-1$,解得$y_6=-2$。
$\therefore P_6(6,-2)$。
求$P_7$:
点$P_6$绕点$C(-2,-1)$旋转$180^\circ$得$P_7$,则$C$是$P_6P_7$的中点。
$\frac{6+x_7}{2}=-2$,解得$x_7=-10$;$\frac{-2+y_7}{2}=-1$,解得$y_7=0$。
$\therefore P_7(-10,0)$。
求$P_8$:
点$P_7$绕点$D(-1,1)$旋转$180^\circ$得$P_8$,则$D$是$P_7P_8$的中点。
$\frac{-10+x_8}{2}=-1$,解得$x_8=8$;$\frac{0+y_8}{2}=1$,解得$y_8=2$。
$\therefore P_8(8,2)$。
规律总结:
观察可得,当$n=4k$时,$P_{4k}(4k,2)$。
求$P_{2024}$:
$2024=4×506$,即$k=506$。
$\therefore x_{2024}=4×506=2024$,$y_{2024}=2$。
$\therefore P_{2024}(2024,2)$。
答案:C
已知$P(0,2)$,即$P_0(0,2)$。
求$P_1$:
点$P$绕点$A(1,1)$旋转$180^\circ$得$P_1$,则$A$是$PP_1$的中点。
$\frac{0+x_1}{2}=1$,解得$x_1=2$;$\frac{2+y_1}{2}=1$,解得$y_1=0$。
$\therefore P_1(2,0)$。
求$P_2$:
点$P_1$绕点$B(2,-1)$旋转$180^\circ$得$P_2$,则$B$是$P_1P_2$的中点。
$\frac{2+x_2}{2}=2$,解得$x_2=2$;$\frac{0+y_2}{2}=-1$,解得$y_2=-2$。
$\therefore P_2(2,-2)$。
求$P_3$:
点$P_2$绕点$C(-2,-1)$旋转$180^\circ$得$P_3$,则$C$是$P_2P_3$的中点。
$\frac{2+x_3}{2}=-2$,解得$x_3=-6$;$\frac{-2+y_3}{2}=-1$,解得$y_3=0$。
$\therefore P_3(-6,0)$。
求$P_4$:
点$P_3$绕点$D(-1,1)$旋转$180^\circ$得$P_4$,则$D$是$P_3P_4$的中点。
$\frac{-6+x_4}{2}=-1$,解得$x_4=4$;$\frac{0+y_4}{2}=1$,解得$y_4=2$。
$\therefore P_4(4,2)$。
求$P_5$:
点$P_4$绕点$A(1,1)$旋转$180^\circ$得$P_5$,则$A$是$P_4P_5$的中点。
$\frac{4+x_5}{2}=1$,解得$x_5=-2$;$\frac{2+y_5}{2}=1$,解得$y_5=0$。
$\therefore P_5(-2,0)$。
求$P_6$:
点$P_5$绕点$B(2,-1)$旋转$180^\circ$得$P_6$,则$B$是$P_5P_6$的中点。
$\frac{-2+x_6}{2}=2$,解得$x_6=6$;$\frac{0+y_6}{2}=-1$,解得$y_6=-2$。
$\therefore P_6(6,-2)$。
求$P_7$:
点$P_6$绕点$C(-2,-1)$旋转$180^\circ$得$P_7$,则$C$是$P_6P_7$的中点。
$\frac{6+x_7}{2}=-2$,解得$x_7=-10$;$\frac{-2+y_7}{2}=-1$,解得$y_7=0$。
$\therefore P_7(-10,0)$。
求$P_8$:
点$P_7$绕点$D(-1,1)$旋转$180^\circ$得$P_8$,则$D$是$P_7P_8$的中点。
$\frac{-10+x_8}{2}=-1$,解得$x_8=8$;$\frac{0+y_8}{2}=1$,解得$y_8=2$。
$\therefore P_8(8,2)$。
规律总结:
观察可得,当$n=4k$时,$P_{4k}(4k,2)$。
求$P_{2024}$:
$2024=4×506$,即$k=506$。
$\therefore x_{2024}=4×506=2024$,$y_{2024}=2$。
$\therefore P_{2024}(2024,2)$。
答案:C
2.[全国初中数学竞赛(广东中山)预赛]在平面直角坐标系内,点A(n,1-n)一定不在(
A.第一象限
B.第二象限
C.第三象限
D.第四象限
C
).A.第一象限
B.第二象限
C.第三象限
D.第四象限
答案:C
解析:
要判断点$A(n,1 - n)$所在象限,需根据各象限内点的坐标特征分析$n$的取值范围:
1. 第一象限:$\begin{cases}n>0\\1 - n>0\end{cases}$,解得$0 < n < 1$,存在$n$使点在第一象限;
2. 第二象限:$\begin{cases}n<0\\1 - n>0\end{cases}$,解得$n < 0$,存在$n$使点在第二象限;
3. 第三象限:$\begin{cases}n<0\\1 - n<0\end{cases}$,由$1 - n < 0$得$n > 1$,与$n < 0$无交集,不存在$n$使点在第三象限;
4. 第四象限:$\begin{cases}n>0\\1 - n<0\end{cases}$,解得$n > 1$,存在$n$使点在第四象限。
综上,点$A$一定不在第三象限。
C
1. 第一象限:$\begin{cases}n>0\\1 - n>0\end{cases}$,解得$0 < n < 1$,存在$n$使点在第一象限;
2. 第二象限:$\begin{cases}n<0\\1 - n>0\end{cases}$,解得$n < 0$,存在$n$使点在第二象限;
3. 第三象限:$\begin{cases}n<0\\1 - n<0\end{cases}$,由$1 - n < 0$得$n > 1$,与$n < 0$无交集,不存在$n$使点在第三象限;
4. 第四象限:$\begin{cases}n>0\\1 - n<0\end{cases}$,解得$n > 1$,存在$n$使点在第四象限。
综上,点$A$一定不在第三象限。
C
3.[全国初中数学竞赛(海南赛区)初赛]已知点P在平面直角坐标系中的坐标为(0,1),O为坐标原点,$\angle QPO= 150^\circ,$且点P到点Q的距离为2,则点Q的坐标为______
$(1,1+\sqrt{3})$或$(-1,1+\sqrt{3})$
.答案:$(1,1+\sqrt{3})$或$(-1,1+\sqrt{3})$
解析:
解:过点Q作QA⊥y轴于点A,
∵点P坐标为(0,1),设Q(x,y),则QA=|x|,PA=|y-1|,PQ=2,∠QPO=150°,
∴∠QPA=180°-150°=30°,
在Rt△QPA中,sin30°=QA/PQ=|x|/2=1/2,cos30°=PA/PQ=|y-1|/2=√3/2,
∴|x|=1,|y-1|=√3,
∵∠QPO=150°,点Q在点P上方,
∴y-1=√3,即y=1+√3,x=±1,
∴点Q的坐标为(1,1+√3)或(-1,1+√3)。
$(1,1+\sqrt{3})$或$(-1,1+\sqrt{3})$
∵点P坐标为(0,1),设Q(x,y),则QA=|x|,PA=|y-1|,PQ=2,∠QPO=150°,
∴∠QPA=180°-150°=30°,
在Rt△QPA中,sin30°=QA/PQ=|x|/2=1/2,cos30°=PA/PQ=|y-1|/2=√3/2,
∴|x|=1,|y-1|=√3,
∵∠QPO=150°,点Q在点P上方,
∴y-1=√3,即y=1+√3,x=±1,
∴点Q的坐标为(1,1+√3)或(-1,1+√3)。
$(1,1+\sqrt{3})$或$(-1,1+\sqrt{3})$
4.(第二十届“希望杯”全国数学邀请赛)记有序的有理数对x,y为(x,y).若xy>0,|x|y - x= 0且|x| + |y|= 3,则满足以上条件的有理数对(x,y)是
(2,1)
或(-2,-1)
.答案:(2,1) (-2,-1) 解析
∵xy>0,
∴x>0,y>0或x<0,y<0.
①当x>0,y>0时,
∵|x|y-x=0,
∴xy-x=0,
∴x(y-1)=0,
∴x=0(舍去)或y-1=0,
∴y=1.
∵|x|+|y|=3,
∴|x|+1=3,
∴|x|=2,
∴x=-2(舍去)或x=2,
∴有理数对(x,y)是(2,1);
②当x<0,y<0时,
∵|x|y-x=0,
∴-xy-x=0,
∴-x(y+1)=0,
∴x=0(舍去)或y+1=0,
∴y=-1.
∵|x|+|y|=3,
∴|x|+1=3,
∴|x|=2,
∴x=-2或x=2(舍去),
∴有理数对(x,y)是(-2,-1).
故满足条件的有理数对(x,y)是(2,1)或(-2,-1).
∵xy>0,
∴x>0,y>0或x<0,y<0.
①当x>0,y>0时,
∵|x|y-x=0,
∴xy-x=0,
∴x(y-1)=0,
∴x=0(舍去)或y-1=0,
∴y=1.
∵|x|+|y|=3,
∴|x|+1=3,
∴|x|=2,
∴x=-2(舍去)或x=2,
∴有理数对(x,y)是(2,1);
②当x<0,y<0时,
∵|x|y-x=0,
∴-xy-x=0,
∴-x(y+1)=0,
∴x=0(舍去)或y+1=0,
∴y=-1.
∵|x|+|y|=3,
∴|x|+1=3,
∴|x|=2,
∴x=-2或x=2(舍去),
∴有理数对(x,y)是(-2,-1).
故满足条件的有理数对(x,y)是(2,1)或(-2,-1).
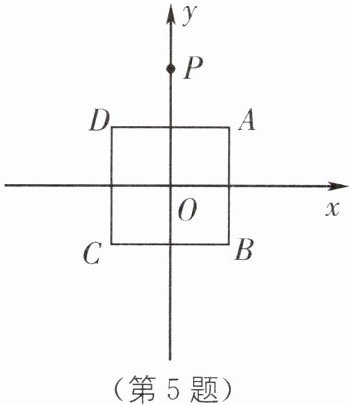
5.[全国初中数学竞赛(湖南赛区)复赛]如图,在平面直角坐标系xOy中,正方形ABCD的中心为坐标原点,顶点A的坐标为(1,1),y轴上一点P(0,2)绕点A旋转180°得到点P1,点P1绕点B旋转180°得到点P2,点P2绕点C旋转180°得点P3,点P3绕点D旋转180°得点P4,…,重复操作依次得到点P1,P2,P3,….求:
(1)点P1,P2,P3的坐标;
(2)点P2024的坐标.
(1)点P1,P2,P3的坐标;
(2)点P2024的坐标.

答案:5.
(1)P₁(2,0),P₂(0,-2),P₃(-2,0).
(2)重复操作依次可得P₄=P₈=P₁₂,P₅=P₉=P₁,P₆=P₁₀=P₂,P₇=P₁₁=P₃.
∵2024=4×506,
∴P₂₀₂₄=P₄.
∴P₂₀₂₄(0,2).
(1)P₁(2,0),P₂(0,-2),P₃(-2,0).
(2)重复操作依次可得P₄=P₈=P₁₂,P₅=P₉=P₁,P₆=P₁₀=P₂,P₇=P₁₁=P₃.
∵2024=4×506,
∴P₂₀₂₄=P₄.
∴P₂₀₂₄(0,2).