9. (2025·陕西商洛期中)如图,长方形ABCD的四个顶点在互相平行的两条直线上,$ AB= 10\ cm $,当点C,D在平行线上同方向匀速运动时,长方形的面积发生了变化.
(1)在这个变化过程中,自变量是______
(2)如果长方形的长BC为x cm,那么请用含x的式子表示长方形ABCD的面积$ y\ cm^2 $.
(3)当长方形的长BC从15 cm变到20 cm时,长方形的面积怎么变化？
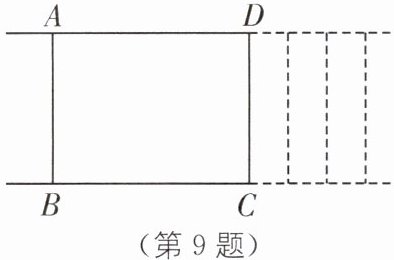
(1)在这个变化过程中,自变量是______
BC（AD）
,因变量是______长方形ABCD的面积
. (2)如果长方形的长BC为x cm,那么请用含x的式子表示长方形ABCD的面积$ y\ cm^2 $.
长方形的面积=AB×BC，即y=10x.
(3)当长方形的长BC从15 cm变到20 cm时,长方形的面积怎么变化？
当BC=15 cm时，y=10x=10×15=150(cm²)，当BC=20 cm时，y=10x=10×20=200(cm²)，所以当长BC从15 cm变到20 cm时，长方形的面积从150 cm²变到200 cm².
答案：（1）BC（AD） 长方形ABCD的面积
（2）长方形的面积=AB×BC，即y=10x.
（3）当BC=15 cm时，y=10x=10×15=150(cm²)，当BC=20 cm时，y=10x=10×20=200(cm²)，所以当长BC从15 cm变到20 cm时，长方形的面积从150 cm²变到200 cm².
（2）长方形的面积=AB×BC，即y=10x.
（3）当BC=15 cm时，y=10x=10×15=150(cm²)，当BC=20 cm时，y=10x=10×20=200(cm²)，所以当长BC从15 cm变到20 cm时，长方形的面积从150 cm²变到200 cm².
11. 如图,自行车每节链条的长度为2.5 cm,交叉重叠部分的圆的直径为0.8 cm.
(1)观察图形,填写下表：
| 链条的节数/节 | 2 | 3 | 4 | … |
| 链条的长度/cm |
(2)如果x节链条的长度是y,那么y与x之间的关系式是什么？
(3)如果一辆某种型号自行车的链条(安装前)由60节这样的链条组成,那么这辆自行车上的链条(安装后)总长度是多少？
(1)观察图形,填写下表：
| 链条的节数/节 | 2 | 3 | 4 | … |
| 链条的长度/cm |
4.2
| 5.9
| 7.6
| … | (2)如果x节链条的长度是y,那么y与x之间的关系式是什么？
y=1.7x+0.8
(3)如果一辆某种型号自行车的链条(安装前)由60节这样的链条组成,那么这辆自行车上的链条(安装后)总长度是多少？
102cm
答案：（1）根据图形，可知
2节链条的长度为2.5×2-0.8=4.2(cm)；
3节链条的长度为2.5×3-0.8×2=5.9(cm)；
4节链条的长度为2.5×4-0.8×3=7.6(cm).
填表如下：
链条的节数/节 2 3 4 …
链条的长度/cm 4.2 5.9 7.6 …
（2）由（1），可得x节链条的长度为y=2.5x-0.8(x-1)=1.7x+0.8.
故y与x之间的关系式是y=1.7x+0.8.
（3）
∵自行车上的链条为环形，在展直的基础上还要缩短0.8 cm，
∴这辆自行车链条的总长度为1.7×60=102(cm).
2节链条的长度为2.5×2-0.8=4.2(cm)；
3节链条的长度为2.5×3-0.8×2=5.9(cm)；
4节链条的长度为2.5×4-0.8×3=7.6(cm).
填表如下：
链条的节数/节 2 3 4 …
链条的长度/cm 4.2 5.9 7.6 …
（2）由（1），可得x节链条的长度为y=2.5x-0.8(x-1)=1.7x+0.8.
故y与x之间的关系式是y=1.7x+0.8.
（3）
∵自行车上的链条为环形，在展直的基础上还要缩短0.8 cm，
∴这辆自行车链条的总长度为1.7×60=102(cm).