1. 7层楼房共有112级台阶,如果每上5级台阶升高1 m,则升高米数h 关于台阶数s 的函数表达式为
$h=\frac{1}{5}s$
,自变量s 的取值范围是$0\leqslant s\leqslant 112$(s 为整数)
.答案:$h=\frac{1}{5}s$ $0\leqslant s\leqslant 112$(s 为整数)
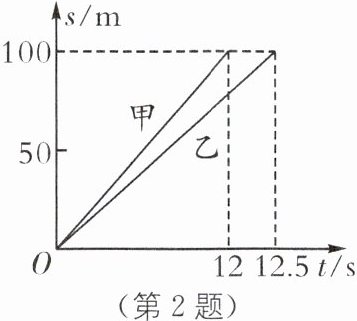
2. 教材P142练习T2·变式 甲、乙两人在赛跑中所行路程s 与时间t 的关系如图所示,回答下列问题:
(1)这是一项多少米的赛跑比赛?
(2)甲、乙两人谁先到达终点?
(3)乙在这次赛跑中的速度为多少?
(1)这是一项多少米的赛跑比赛?
(2)甲、乙两人谁先到达终点?
(3)乙在这次赛跑中的速度为多少?

答案:
(1)由图象,得这是一项 100 m 的赛跑比赛.
(2)由图象,得甲先到达终点.
(3)由图象,得乙在这次赛跑中的速度是 $100÷ 12.5=8(m/s)$.
(1)由图象,得这是一项 100 m 的赛跑比赛.
(2)由图象,得甲先到达终点.
(3)由图象,得乙在这次赛跑中的速度是 $100÷ 12.5=8(m/s)$.
3. “十一”期间,小华一家人开车到距家100 千米的景点旅游,出发前,汽车油箱内储油45 升,当行驶60 千米时,发现油箱剩余油量为31.5 升(假设行驶过程中汽车的耗油量是均匀的).
(1)求该车平均每千米的耗油量.
(2)写出剩余油量Q(升)与行驶路程x(千米)之间的函数表达式.
(3)当油箱中剩余油量低于3 升时,汽车将自动报警,若往返途中不加油,他们能否在汽车报警前回到家?请说明理由.
(1)求该车平均每千米的耗油量.
(2)写出剩余油量Q(升)与行驶路程x(千米)之间的函数表达式.
(3)当油箱中剩余油量低于3 升时,汽车将自动报警,若往返途中不加油,他们能否在汽车报警前回到家?请说明理由.
答案:
(1)$\frac{45-31.5}{60}=0.225(升)$.
故该车平均每千米耗油 0.225 升.
(2)$Q=45-0.225x$.
(3)当$x=200$时,$Q=45-0.225× 200=0$.
$\because 0<3$,
∴他们不能在汽车报警前回到家.
(1)$\frac{45-31.5}{60}=0.225(升)$.
故该车平均每千米耗油 0.225 升.
(2)$Q=45-0.225x$.
(3)当$x=200$时,$Q=45-0.225× 200=0$.
$\because 0<3$,
∴他们不能在汽车报警前回到家.
4. 新情境 荡秋千 (2025·山东济南长清区期末)小红帮弟弟荡秋千(如图(1)),秋千离地面的高度h(m)与摆动时间t(s)之间的关系如图(2)所示.

(1)根据函数的定义,变量h
(2)结合图象回答:
①当t= 0.7 s时,h 的值是
②秋千摆动第二个来回需多少时间?

(1)根据函数的定义,变量h
是
(填“是”或者“不是”)关于t 的函数,变量h 的取值范围是0.5≤h≤1.5
.(2)结合图象回答:
①当t= 0.7 s时,h 的值是
0.5
,它的实际意义是摆动时间为 0.7 s 时,秋千离地面的高度是 0.5 m
.②秋千摆动第二个来回需多少时间?
2.6 s.
答案:
(1)是 $0.5\leqslant h\leqslant 1.5$
(2)①0.5 摆动时间为 0.7 s 时,秋千离地面的高度是 0.5 m
②2.6 s.
(1)是 $0.5\leqslant h\leqslant 1.5$
(2)①0.5 摆动时间为 0.7 s 时,秋千离地面的高度是 0.5 m
②2.6 s.