8. 三条互不重合的直线的交点个数可能是(
A.0,1,3
B.0,2,3
C.0,1,2,3
D.0,1,2
C
)A.0,1,3
B.0,2,3
C.0,1,2,3
D.0,1,2
答案:C
解析:
解:三条互不重合的直线交点个数情况如下:
1. 三条直线平行,交点个数为0;
2. 三条直线相交于一点,交点个数为1;
3. 两条直线平行,第三条直线与它们相交,交点个数为2;
4. 三条直线两两相交且不交于同一点,交点个数为3。
综上,交点个数可能是0,1,2,3。
答案:C
1. 三条直线平行,交点个数为0;
2. 三条直线相交于一点,交点个数为1;
3. 两条直线平行,第三条直线与它们相交,交点个数为2;
4. 三条直线两两相交且不交于同一点,交点个数为3。
综上,交点个数可能是0,1,2,3。
答案:C
9. 若平面内有3个点,过其中任意两点画直线,最多可画
3
条直线;若平面内有4个点,过其中任意两点画直线,最多可画6
条直线;若平面内有5个点,过其中任意两点画直线,最多可画10
条直线;…;若平面内有n个点,过其中任意两点画直线,最多可画$\frac{n(n - 1)}{2}$
条直线.答案:3 6 10 $\frac{n(n - 1)}{2}$
解析:
3;6;10;$\frac{n(n - 1)}{2}$
10. 按下列语句画出图形:
(1)直线l经过A,B,C三点,点C在点A与点B之间;
(2)直线a,b,c相交于点O;
(3)直线AB与CD相交于点P;
(4)P是直线a外一点,经过点P有一条直线b与直线a相交于点Q.
(1)直线l经过A,B,C三点,点C在点A与点B之间;
(2)直线a,b,c相交于点O;
(3)直线AB与CD相交于点P;
(4)P是直线a外一点,经过点P有一条直线b与直线a相交于点Q.
答案:
解:(1)如答图①.

(2)如答图②.

(3)如答图③.

(4)如答图④.
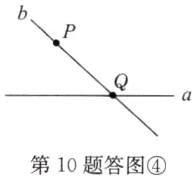
解:(1)如答图①.

(2)如答图②.

(3)如答图③.

(4)如答图④.

11. 如图,有A,B,C,D四个村庄,为解决当地缺水问题,政府准备投资修建一个蓄水池,不考虑其他因素,请你画图确定蓄水池H的位置,使它与四个村庄的距离之和最小.
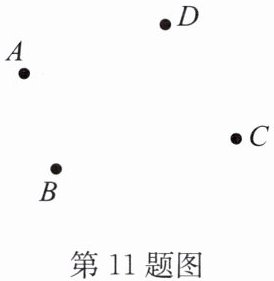

答案:
解:如答图,连接AC,BD,它们的交点是H,点H就是修建蓄水池的位置,这一点到A,B,C,D四个村庄的距离之和最小.

解:如答图,连接AC,BD,它们的交点是H,点H就是修建蓄水池的位置,这一点到A,B,C,D四个村庄的距离之和最小.

12. 如图,数一数每个图形的线段总数:
(1)如图①,线段总数是2+1=
(2)如图②,线段总数是3+2+1=
(3)如图③,线段总数是4+3+2+1=
(4)如图④,线段总数是5+4+3+2+1=
(5)由此得出求线段总数的规律:当线段上共有n个点(包括两个端点)时,线段的总数为
(6)由以上规律,解答问题:如果10位同学聚会,每两位同学都要握手一次,一共需要握多少次手?

(1)如图①,线段总数是2+1=
3
;(2)如图②,线段总数是3+2+1=
6
;(3)如图③,线段总数是4+3+2+1=
10
;(4)如图④,线段总数是5+4+3+2+1=
15
;(5)由此得出求线段总数的规律:当线段上共有n个点(包括两个端点)时,线段的总数为
$\frac{n(n - 1)}{2}$
,当n= 22时,线段的总数为231
;(6)由以上规律,解答问题:如果10位同学聚会,每两位同学都要握手一次,一共需要握多少次手?

解:$\frac{10×9}{2}$=45(次).答:一共需要握45次手.
答案:(1)3 (2)6 (3)10 (4)15 (5)$\frac{n(n - 1)}{2}$ 231
(6)解:$\frac{10×9}{2}$=45(次).答:一共需要握45次手.
(6)解:$\frac{10×9}{2}$=45(次).答:一共需要握45次手.