1. 下列说法错误的是(
A.画线段$AB= 2$厘米
B.延长线段$AB到点C$,使得$AC= 2AB$
C.画射线$AB= 2$厘米
D.在射线$AC上截取AB= 2$厘米
C
)A.画线段$AB= 2$厘米
B.延长线段$AB到点C$,使得$AC= 2AB$
C.画射线$AB= 2$厘米
D.在射线$AC上截取AB= 2$厘米
答案:C
2. 如图,线段$AB= DE$,$C为线段AE$的中点,下列式子不正确的是(
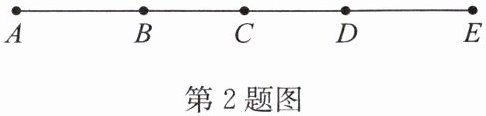
A.$BC= CD$
B.$CD= \frac {1}{2}AE-AB$
C.$CD= AD-CE$
D.$CD= DE$
D
)
A.$BC= CD$
B.$CD= \frac {1}{2}AE-AB$
C.$CD= AD-CE$
D.$CD= DE$
答案:D
解析:
解:
∵C为线段AE的中点,
∴AC=CE=1/2AE。
∵AB=DE,设AB=DE=x,AC=CE=y,
则AE=2y,AD=AC+CD=y+CD,
BC=AC-AB=y-x,CD=CE-DE=y-x,
∴BC=CD(A正确)。
CD=CE-DE=1/2AE-AB(B正确)。
CD=AD-AC=AD-CE(C正确)。
CD=y-x,DE=x,无法确定CD=DE(D不正确)。
答案:D
∵C为线段AE的中点,
∴AC=CE=1/2AE。
∵AB=DE,设AB=DE=x,AC=CE=y,
则AE=2y,AD=AC+CD=y+CD,
BC=AC-AB=y-x,CD=CE-DE=y-x,
∴BC=CD(A正确)。
CD=CE-DE=1/2AE-AB(B正确)。
CD=AD-AC=AD-CE(C正确)。
CD=y-x,DE=x,无法确定CD=DE(D不正确)。
答案:D
3. 已知点$C在射线AB$上,若$AB= 3$,$BC= 2$,则$AC$的长为
1或5
.答案:1或5
解析:
解:
情况一:点C在点B右侧时,AC=AB+BC=3+2=5;
情况二:点C在点A、B之间时,AC=AB-BC=3-2=1。
AC的长为1或5。
情况一:点C在点B右侧时,AC=AB+BC=3+2=5;
情况二:点C在点A、B之间时,AC=AB-BC=3-2=1。
AC的长为1或5。
4. 如图,已知线段$AB= 16cm$,$O是线段AB$的中点,点$C在线段AB$上,$BC= \frac {5}{3}AC$,$P是线段AC$的中点,则线段$OP$的长为
5
$cm$.答案:5
解析:
解:设 $ AC = x \, cm $,则 $ BC = \frac{5}{3}x \, cm $。
因为 $ AB = AC + BC = 16 \, cm $,
所以 $ x + \frac{5}{3}x = 16 $,解得 $ x = 6 $,即 $ AC = 6 \, cm $。
因为 $ P $ 是 $ AC $ 的中点,所以 $ AP = PC = \frac{1}{2}AC = 3 \, cm $。
因为 $ O $ 是 $ AB $ 的中点,所以 $ AO = \frac{1}{2}AB = 8 \, cm $。
所以 $ OP = AO - AP = 8 - 3 = 5 \, cm $。
5
因为 $ AB = AC + BC = 16 \, cm $,
所以 $ x + \frac{5}{3}x = 16 $,解得 $ x = 6 $,即 $ AC = 6 \, cm $。
因为 $ P $ 是 $ AC $ 的中点,所以 $ AP = PC = \frac{1}{2}AC = 3 \, cm $。
因为 $ O $ 是 $ AB $ 的中点,所以 $ AO = \frac{1}{2}AB = 8 \, cm $。
所以 $ OP = AO - AP = 8 - 3 = 5 \, cm $。
5
5. (2024·建邺区期末)已知线段$AB= 5cm$,延长$AB到点C$,$D是AC$的中点,$BD= 1cm$,则线段$AC$的长是
8或12
$cm$.答案:8或12
解析:
解:设线段$AC$的长为$x$cm。
因为$D$是$AC$的中点,所以$AD = \frac{1}{2}AC=\frac{x}{2}$cm。
情况一:点$C$在$AB$的延长线上($B$在$A$、$C$之间)
此时$AD = AB + BD$,已知$AB = 5$cm,$BD = 1$cm,
则$\frac{x}{2}=5 + 1$,解得$x = 12$。
情况二:点$C$在$BA$的延长线上($A$在$B$、$C$之间)
此时$AD = AB - BD$,
则$\frac{x}{2}=5 - 1$,解得$x = 8$。
综上,线段$AC$的长是$8$或$12$cm。
答案:$8$或$12$
因为$D$是$AC$的中点,所以$AD = \frac{1}{2}AC=\frac{x}{2}$cm。
情况一:点$C$在$AB$的延长线上($B$在$A$、$C$之间)
此时$AD = AB + BD$,已知$AB = 5$cm,$BD = 1$cm,
则$\frac{x}{2}=5 + 1$,解得$x = 12$。
情况二:点$C$在$BA$的延长线上($A$在$B$、$C$之间)
此时$AD = AB - BD$,
则$\frac{x}{2}=5 - 1$,解得$x = 8$。
综上,线段$AC$的长是$8$或$12$cm。
答案:$8$或$12$
6. 如果线段$AB= 12cm$,$MA+MB= 16cm$,那么下列说法正确的是(
A.点$M在线段AB$上
B.点$M在直线AB$上
C.点$M在直线AB$外
D.点$M可能在直线AB$上,也可能在直线$AB$外
D
)A.点$M在线段AB$上
B.点$M在直线AB$上
C.点$M在直线AB$外
D.点$M可能在直线AB$上,也可能在直线$AB$外
答案:D
解析:
解:
若点M在直线AB上:
当M在AB延长线上时,设AM = x,则MB = x - 12,由MA + MB = x + (x - 12) = 16,解得x = 14,存在;
当M在BA延长线上时,同理可得存在点M。
若点M在直线AB外:
以A、B为焦点,MA + MB = 16cm(16 > 12),根据椭圆定义,点M的轨迹为椭圆上的点,存在。
综上,点M可能在直线AB上,也可能在直线AB外。
答案:D
若点M在直线AB上:
当M在AB延长线上时,设AM = x,则MB = x - 12,由MA + MB = x + (x - 12) = 16,解得x = 14,存在;
当M在BA延长线上时,同理可得存在点M。
若点M在直线AB外:
以A、B为焦点,MA + MB = 16cm(16 > 12),根据椭圆定义,点M的轨迹为椭圆上的点,存在。
综上,点M可能在直线AB上,也可能在直线AB外。
答案:D
7. 延长线段$AB到点C$,使得$BC= 3AB$,取线段$AC的中点D$,有下列结论:①$B是线段AD$的中点;②$BD= \frac {1}{2}CD$;③$AB= CD$;④$BC-AD= AB$.其中正确的是(
A.①②③
B.①②④
C.①③④
D.②③④
B
)A.①②③
B.①②④
C.①③④
D.②③④
答案:B
解析:
解:设 $ AB = x $,则 $ BC = 3AB = 3x $。
$ AC = AB + BC = x + 3x = 4x $。
$ D $ 是 $ AC $ 中点,$ AD = \frac{1}{2}AC = 2x $。
① $ AD = 2x $,$ AB = x $,则 $ BD = AD - AB = x $,$ AB = BD = x $,故 $ B $ 是 $ AD $ 中点,①正确。
② $ CD = AD = 2x $,$ BD = x $,$ BD = \frac{1}{2}CD $($ x = \frac{1}{2} × 2x $),②正确。
③ $ AB = x $,$ CD = 2x $,$ AB \neq CD $,③错误。
④ $ BC - AD = 3x - 2x = x = AB $,④正确。
综上,正确的是①②④。
答案:B
$ AC = AB + BC = x + 3x = 4x $。
$ D $ 是 $ AC $ 中点,$ AD = \frac{1}{2}AC = 2x $。
① $ AD = 2x $,$ AB = x $,则 $ BD = AD - AB = x $,$ AB = BD = x $,故 $ B $ 是 $ AD $ 中点,①正确。
② $ CD = AD = 2x $,$ BD = x $,$ BD = \frac{1}{2}CD $($ x = \frac{1}{2} × 2x $),②正确。
③ $ AB = x $,$ CD = 2x $,$ AB \neq CD $,③错误。
④ $ BC - AD = 3x - 2x = x = AB $,④正确。
综上,正确的是①②④。
答案:B
8. 互不重合的三点$A$,$B$,$C$在同一条直线上,已知$AC= 2a+1$,$BC= a+4$,$AB= 3a$,这三点的位置关系是(
A.点$A在B$,$C$两点之间
B.点$B在A$,$C$两点之间
C.点$C在A$,$B$两点之间
D.无法确定
A
)A.点$A在B$,$C$两点之间
B.点$B在A$,$C$两点之间
C.点$C在A$,$B$两点之间
D.无法确定
答案:A
解析:
解:
∵ 三点互不重合且共线,
∴ 分三种情况讨论:
情况1:点A在B,C两点之间
则 $ AB + AC = BC $,
即 $ 3a + (2a + 1) = a + 4 $,
解得 $ 4a = 3 $,$ a = \frac{3}{4} $。
此时 $ AC = 2×\frac{3}{4} + 1 = \frac{5}{2} $,$ BC = \frac{3}{4} + 4 = \frac{19}{4} $,$ AB = 3×\frac{3}{4} = \frac{9}{4} $,均为正数,符合题意。
情况2:点B在A,C两点之间
则 $ AB + BC = AC $,
即 $ 3a + (a + 4) = 2a + 1 $,
解得 $ 2a = -3 $,$ a = -\frac{3}{2} $。
此时 $ AB = 3×(-\frac{3}{2}) = -\frac{9}{2} $,线段长度不能为负,不合题意,舍去。
情况3:点C在A,B两点之间
则 $ AC + BC = AB $,
即 $ (2a + 1) + (a + 4) = 3a $,
化简得 $ 3a + 5 = 3a $,$ 5 = 0 $,无解。
综上,只有情况1成立,即点A在B,C两点之间。
答案:A
∵ 三点互不重合且共线,
∴ 分三种情况讨论:
情况1:点A在B,C两点之间
则 $ AB + AC = BC $,
即 $ 3a + (2a + 1) = a + 4 $,
解得 $ 4a = 3 $,$ a = \frac{3}{4} $。
此时 $ AC = 2×\frac{3}{4} + 1 = \frac{5}{2} $,$ BC = \frac{3}{4} + 4 = \frac{19}{4} $,$ AB = 3×\frac{3}{4} = \frac{9}{4} $,均为正数,符合题意。
情况2:点B在A,C两点之间
则 $ AB + BC = AC $,
即 $ 3a + (a + 4) = 2a + 1 $,
解得 $ 2a = -3 $,$ a = -\frac{3}{2} $。
此时 $ AB = 3×(-\frac{3}{2}) = -\frac{9}{2} $,线段长度不能为负,不合题意,舍去。
情况3:点C在A,B两点之间
则 $ AC + BC = AB $,
即 $ (2a + 1) + (a + 4) = 3a $,
化简得 $ 3a + 5 = 3a $,$ 5 = 0 $,无解。
综上,只有情况1成立,即点A在B,C两点之间。
答案:A
9. 如图,有公共端点$P的两条线段MP$,$NP组成一条折线M-P-N$,若该折线$M-P-N上一点Q$把这条折线分成相等的两部分,我们把这个点$Q$叫作这条折线的“折中点”.已知$D是折线A-C-B$的“折中点”,$E为线段AC$的中点,$CD= 1$,$CE= 3$,则线段$BC$的长为
8或4
.答案:8或4
解析:
解:
∵E为线段AC的中点,CE=3,
∴AC=2CE=6。
情况1:点D在AC上
∵CD=1,
∴AD=AC-CD=6-1=5,
折线A-C-B的长度为AD+DC+CB=AC+CB=6+BC,
折中点D将折线分为两部分,每部分长度为(6+BC)/2,
又AD=5=(6+BC)/2,
解得BC=4。
情况2:点D在BC上
∵CD=1,
∴AD=AC+CD=6+1=7,
折线A-C-B的长度为AC+CB=6+BC,
折中点D将折线分为两部分,每部分长度为(6+BC)/2,
又AD=7=(6+BC)/2,
解得BC=8。
综上,BC的长为8或4。
答案:8或4
∵E为线段AC的中点,CE=3,
∴AC=2CE=6。
情况1:点D在AC上
∵CD=1,
∴AD=AC-CD=6-1=5,
折线A-C-B的长度为AD+DC+CB=AC+CB=6+BC,
折中点D将折线分为两部分,每部分长度为(6+BC)/2,
又AD=5=(6+BC)/2,
解得BC=4。
情况2:点D在BC上
∵CD=1,
∴AD=AC+CD=6+1=7,
折线A-C-B的长度为AC+CB=6+BC,
折中点D将折线分为两部分,每部分长度为(6+BC)/2,
又AD=7=(6+BC)/2,
解得BC=8。
综上,BC的长为8或4。
答案:8或4
10. 已知线段$AB$,在线段$AB的延长线上取一点C$,使$AC= 2BC$.在线段$AB的反向延长线上取一点D$,使$DA= 2AB$,那么线段$AC的长是线段DB$长的
$\frac{2}{3}$
.答案:$\frac{2}{3}$
解析:
设线段$AB$的长为$x$。
因为点$C$在$AB$的延长线上,且$AC = 2BC$,又因为$AC=AB + BC$,所以$AB + BC=2BC$,即$x+BC = 2BC$,解得$BC=x$,则$AC=AB + BC=x+x = 2x$。
因为点$D$在$AB$的反向延长线上,且$DA = 2AB$,所以$DA=2x$,则$DB=DA + AB=2x+x = 3x$。
所以$\frac{AC}{DB}=\frac{2x}{3x}=\frac{2}{3}$。
$\frac{2}{3}$
因为点$C$在$AB$的延长线上,且$AC = 2BC$,又因为$AC=AB + BC$,所以$AB + BC=2BC$,即$x+BC = 2BC$,解得$BC=x$,则$AC=AB + BC=x+x = 2x$。
因为点$D$在$AB$的反向延长线上,且$DA = 2AB$,所以$DA=2x$,则$DB=DA + AB=2x+x = 3x$。
所以$\frac{AC}{DB}=\frac{2x}{3x}=\frac{2}{3}$。
$\frac{2}{3}$