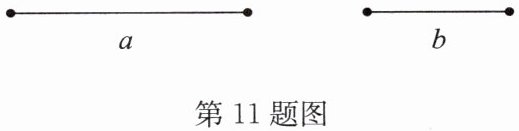
11. 如图,已知线段$a$,$b$,用直尺和圆规求作一条线段$c$,使$c= 2a-b$.
答案：
解:先画出一条线段$AD = 2a$，再在$AD$上截取$CD = b$，线段$AC$即为所求线段，如答图。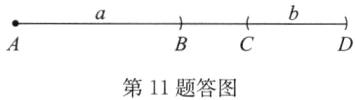
解:先画出一条线段$AD = 2a$，再在$AD$上截取$CD = b$，线段$AC$即为所求线段，如答图。
12. (2024·宜兴月考)如图,线段$AB= 24$.$C是线段AB$的中点,$D是线段BC$的中点.
(1)求线段$AD$的长；
(2)在线段$AD上有一点E$,满足$CE= \frac {1}{6}BC$,求$AE$的长.
(1)求线段$AD$的长；
(2)在线段$AD上有一点E$,满足$CE= \frac {1}{6}BC$,求$AE$的长.
答案：(1)因为$C$是线段$AB$的中点，所以$AC = BC = \frac{1}{2}AB = \frac{1}{2}×24 = 12$。因为$D$是线段$BC$的中点，所以$CD = BD = \frac{1}{2}BC = \frac{1}{2}×12 = 6$，所以$AD = AC + CD = 12 + 6 = 18$。(2)因为$AC = BC = 12$，所以$CE = \frac{1}{6}BC = \frac{1}{6}×12 = 2$，当点$E$在线段$AC$上时，$AE = AC - CE = 12 - 2 = 10$；当点$E$在线段$CD$上时，$AE = AC + CE = 12 + 2 = 14$。综上所述，$AE$的长为10或14。
13. 已知$C为线段AB$的中点,$D为线段AC$的中点,解答下列问题：
(1)画出相应的图形,并写出图中所有的线段；
(2)若图中所有线段的长度和为$26$,求线段$AC$的长度；
(3)若$E为线段BC$上的点,$M为线段EB$的中点,$DM= a$,$CE= b$,求线段$AB$的长度.(用含$a$,$b$的代数式表示)
(1)画出相应的图形,并写出图中所有的线段；
(2)若图中所有线段的长度和为$26$,求线段$AC$的长度；
(3)若$E为线段BC$上的点,$M为线段EB$的中点,$DM= a$,$CE= b$,求线段$AB$的长度.(用含$a$,$b$的代数式表示)
答案：
(1)如答图①。
线段为$AD$，$AC$，$AB$，$DC$，$DB$，$CB$。(2)因为$C$，$D$分别是线段$AB$，$AC$的中点，所以$AB = 2AC$，$AC = 2AD$，设$AC = x$，则有$\frac{1}{2}x + x + 2x + \frac{1}{2}x + \frac{3}{2}x + x = 26$，解得$x = 4$，即$AC = 4$。(3)如答图②。
因为$M$为线段$EB$的中点，所以$EB = 2EM$，所以$AB = AC + EB + CE = 2CD + 2EM + CE = 2(DC + EM) + CE = 2(DM - CE) + CE = 2DM - CE$。因为$DM = a$，$CE = b$，所以$AB = 2a - b$。
(1)如答图①。
线段为$AD$，$AC$，$AB$，$DC$，$DB$，$CB$。(2)因为$C$，$D$分别是线段$AB$，$AC$的中点，所以$AB = 2AC$，$AC = 2AD$，设$AC = x$，则有$\frac{1}{2}x + x + 2x + \frac{1}{2}x + \frac{3}{2}x + x = 26$，解得$x = 4$，即$AC = 4$。(3)如答图②。 因为$M$为线段$EB$的中点，所以$EB = 2EM$，所以$AB = AC + EB + CE = 2CD + 2EM + CE = 2(DC + EM) + CE = 2(DM - CE) + CE = 2DM - CE$。因为$DM = a$，$CE = b$，所以$AB = 2a - b$。14. (1)如图,点$C在线段AB$上,且$AC= 6cm$,$BC= 4cm$,$M是线段AC$的中点,$N是线段BC$的中点,求线段$MN$的长；
(2)在(1)中,若$AC= a cm$,$BC= b cm$,其他条件不变,你能求出线段$MN$的长度吗？(用含$a$,$b$的代数式表示)
(3)对于(1),若我们这样叙述：“点$C在直线AB$上,且$AC= 6cm$,$BC= 4cm$,$M$,$N分别是AC$,$BC$的中点,求线段$MN$的长.”结果会变化吗？为什么？
(2)在(1)中,若$AC= a cm$,$BC= b cm$,其他条件不变,你能求出线段$MN$的长度吗？(用含$a$,$b$的代数式表示)
(3)对于(1),若我们这样叙述：“点$C在直线AB$上,且$AC= 6cm$,$BC= 4cm$,$M$,$N分别是AC$,$BC$的中点,求线段$MN$的长.”结果会变化吗？为什么？
答案：(1)$MN = CM + CN = \frac{1}{2}AC + \frac{1}{2}BC = \frac{1}{2}×6 + \frac{1}{2}×4 = 5(cm)$。(2)$MN = CM + CN = \frac{1}{2}AC + \frac{1}{2}BC = \frac{1}{2}a + \frac{1}{2}b = \frac{1}{2}(a + b)cm$。(3)会变化。当点$C$在线段$AB$上时，$MN = \frac{1}{2}(AC + BC) = \frac{1}{2}×(6 + 4) = 5(cm)$；当点$C$在线段$AB$外(即点$C$在线段$AB$的延长线上)时，$MN = \frac{1}{2}(AC - BC) = \frac{1}{2}×(6 - 4) = 1(cm)$。即$MN$的长为5cm或1cm。
解析：
(1)解：因为M是线段AC的中点，AC=6cm，所以CM=$\frac{1}{2}$AC=$\frac{1}{2}$×6=3cm。
因为N是线段BC的中点，BC=4cm，所以CN=$\frac{1}{2}$BC=$\frac{1}{2}$×4=2cm。
所以MN=CM+CN=3+2=5cm。
(2)解：因为M是线段AC的中点，AC=a cm，所以CM=$\frac{1}{2}$AC=$\frac{1}{2}$a cm。
因为N是线段BC的中点，BC=b cm，所以CN=$\frac{1}{2}$BC=$\frac{1}{2}$b cm。
所以MN=CM+CN=$\frac{1}{2}$a+$\frac{1}{2}$b=$\frac{1}{2}$(a+b)cm。
(3)解：会变化。
情况1：当点C在线段AB上时，MN=$\frac{1}{2}$(AC+BC)=$\frac{1}{2}$×(6+4)=5cm。
情况2：当点C在线段AB的延长线上时，MN=$\frac{1}{2}$(AC-BC)=$\frac{1}{2}$×(6-4)=1cm。
综上，MN的长为5cm或1cm。
因为N是线段BC的中点，BC=4cm，所以CN=$\frac{1}{2}$BC=$\frac{1}{2}$×4=2cm。
所以MN=CM+CN=3+2=5cm。
(2)解：因为M是线段AC的中点，AC=a cm，所以CM=$\frac{1}{2}$AC=$\frac{1}{2}$a cm。
因为N是线段BC的中点，BC=b cm，所以CN=$\frac{1}{2}$BC=$\frac{1}{2}$b cm。
所以MN=CM+CN=$\frac{1}{2}$a+$\frac{1}{2}$b=$\frac{1}{2}$(a+b)cm。
(3)解：会变化。
情况1：当点C在线段AB上时，MN=$\frac{1}{2}$(AC+BC)=$\frac{1}{2}$×(6+4)=5cm。
情况2：当点C在线段AB的延长线上时，MN=$\frac{1}{2}$(AC-BC)=$\frac{1}{2}$×(6-4)=1cm。
综上，MN的长为5cm或1cm。