10. 已知一个角的补角比这个角的余角的 4 倍小$30^{\circ}$,求这个角的度数。
答案:解:设这个角的度数是x. 根据题意,得
180° - x + 30° = 4(90° - x),
解得x = 50°.
答:这个角的度数为50°.
180° - x + 30° = 4(90° - x),
解得x = 50°.
答:这个角的度数为50°.
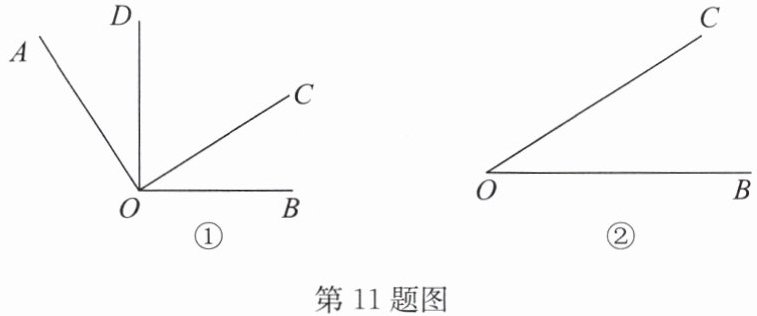
11. 如图①,$∠AOC和∠BOD$都是直角。
(1)如果$∠DOC = 35^{\circ}$,那么$∠AOB = $______;
(2)找出图①中一组相等的锐角______;
(3)若$∠DOC$变小,则$∠AOB$将______;(填“变大”或“变小”)
(4)利用能够画直角的工具在图②中再画一个与$∠BOC$相等的角,不写作法,保留作图痕迹。
(1)如果$∠DOC = 35^{\circ}$,那么$∠AOB = $______;
(2)找出图①中一组相等的锐角______;
(3)若$∠DOC$变小,则$∠AOB$将______;(填“变大”或“变小”)
(4)利用能够画直角的工具在图②中再画一个与$∠BOC$相等的角,不写作法,保留作图痕迹。

答案:
(1)145° (2)∠AOD = ∠BOC (3)变大
(4)解:如答图,∠EOF即为所求.

(1)145° (2)∠AOD = ∠BOC (3)变大
(4)解:如答图,∠EOF即为所求.

12. 已知$O为直线AB$上一点。
(1)如图①,过点$O作射线OC$,使$∠AOC : ∠BOC = 3 : 2$,求$∠AOC与∠BOC$的度数;
(2)如图②,射线$OC为∠AOB$内部任意一条射线,且$∠COE = ∠BOE$,$∠COD = ∠AOD$,则$∠DOE = $______$^{\circ}$,此时图中互余的角有______对,互补的角有______对;
(3)如图③,在(2)的情况下,保持$∠DOE$的度数不变,改变其他条件,使得$∠COD = ∠BOC$,此时$∠AOD与∠COE$满足怎样的数量关系?并说明理由。

(1)
(2)
(3)
(1)如图①,过点$O作射线OC$,使$∠AOC : ∠BOC = 3 : 2$,求$∠AOC与∠BOC$的度数;
(2)如图②,射线$OC为∠AOB$内部任意一条射线,且$∠COE = ∠BOE$,$∠COD = ∠AOD$,则$∠DOE = $______$^{\circ}$,此时图中互余的角有______对,互补的角有______对;
(3)如图③,在(2)的情况下,保持$∠DOE$的度数不变,改变其他条件,使得$∠COD = ∠BOC$,此时$∠AOD与∠COE$满足怎样的数量关系?并说明理由。

(1)
解:因为∠AOC : ∠BOC = 3 : 2,
所以设∠AOC = 3x,则∠BOC = 2x,
根据题意,得3x + 2x = 180°,解得x = 36°,
所以∠AOC = 108°,∠BOC = 72°.
所以设∠AOC = 3x,则∠BOC = 2x,
根据题意,得3x + 2x = 180°,解得x = 36°,
所以∠AOC = 108°,∠BOC = 72°.
(2)
90
4
5
(3)
解:∠AOD = 2∠COE. 理由如下:
因为∠COD = ∠BOC,
所以∠BOC = $\frac{1}{2}$∠BOD = $\frac{1}{2}$(180° - ∠AOD) = 90° - $\frac{1}{2}$∠AOD.
因为∠AOD + ∠DOC + ∠BOC = 180°,
所以∠AOD + (90° - ∠COE) + (90° - $\frac{1}{2}$∠AOD) = 180°,
所以∠AOD = 2∠COE.
因为∠COD = ∠BOC,
所以∠BOC = $\frac{1}{2}$∠BOD = $\frac{1}{2}$(180° - ∠AOD) = 90° - $\frac{1}{2}$∠AOD.
因为∠AOD + ∠DOC + ∠BOC = 180°,
所以∠AOD + (90° - ∠COE) + (90° - $\frac{1}{2}$∠AOD) = 180°,
所以∠AOD = 2∠COE.
答案:(1)解:因为∠AOC : ∠BOC = 3 : 2,
所以设∠AOC = 3x,则∠BOC = 2x,
根据题意,得3x + 2x = 180°,解得x = 36°,
所以∠AOC = 108°,∠BOC = 72°.
(2)90 4 5
(3)解:∠AOD = 2∠COE. 理由如下:
因为∠COD = ∠BOC,
所以∠BOC = $\frac{1}{2}$∠BOD = $\frac{1}{2}$(180° - ∠AOD) = 90° - $\frac{1}{2}$∠AOD.
因为∠AOD + ∠DOC + ∠BOC = 180°,
所以∠AOD + (90° - ∠COE) + (90° - $\frac{1}{2}$∠AOD) = 180°,
所以∠AOD = 2∠COE.
所以设∠AOC = 3x,则∠BOC = 2x,
根据题意,得3x + 2x = 180°,解得x = 36°,
所以∠AOC = 108°,∠BOC = 72°.
(2)90 4 5
(3)解:∠AOD = 2∠COE. 理由如下:
因为∠COD = ∠BOC,
所以∠BOC = $\frac{1}{2}$∠BOD = $\frac{1}{2}$(180° - ∠AOD) = 90° - $\frac{1}{2}$∠AOD.
因为∠AOD + ∠DOC + ∠BOC = 180°,
所以∠AOD + (90° - ∠COE) + (90° - $\frac{1}{2}$∠AOD) = 180°,
所以∠AOD = 2∠COE.