9. 如图,已知$OM// a,ON// a$,所以O,M,N三点共线. 理由是
过直线外一点有且只有一条直线与这条直线平行
.答案:过直线外一点有且只有一条直线与这条直线平行
10. 经过已知直线外三点作已知直线的平行线,可以作
1 或 2 或 3
条.答案:1 或 2 或 3
解析:
解:分三种情况:
1. 若三点中有两点所在直线与已知直线平行,则只能作1条平行线;
2. 若三点中任意两点所在直线都不与已知直线平行,且三点共线,则可作1条平行线;若三点不共线,且其中两点确定的直线与已知直线平行,另一点确定的直线也与已知直线平行,则可作2条平行线;
3. 若三点中任意两点确定的直线都不与已知直线平行,且三点不共线,且过这三点能作出三条不同的直线与已知直线平行,则可作3条平行线。
综上,可以作1或2或3条。
答案:1 或 2 或 3
1. 若三点中有两点所在直线与已知直线平行,则只能作1条平行线;
2. 若三点中任意两点所在直线都不与已知直线平行,且三点共线,则可作1条平行线;若三点不共线,且其中两点确定的直线与已知直线平行,另一点确定的直线也与已知直线平行,则可作2条平行线;
3. 若三点中任意两点确定的直线都不与已知直线平行,且三点不共线,且过这三点能作出三条不同的直线与已知直线平行,则可作3条平行线。
综上,可以作1或2或3条。
答案:1 或 2 或 3
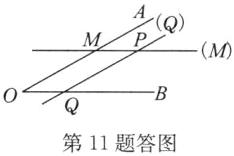
11. (1)按下列语句作图:
①任意作一个$∠AOB$;②在角内部取一点P;③过点P分别作$PQ// OA,PM// OB$.
(2)在(1)所作的图中,若$∠AOB= 30^{\circ }$,猜想$∠MPQ$的度数.(不用说明理由)
①任意作一个$∠AOB$;②在角内部取一点P;③过点P分别作$PQ// OA,PM// OB$.
(2)在(1)所作的图中,若$∠AOB= 30^{\circ }$,猜想$∠MPQ$的度数.(不用说明理由)
答案:
(1)如答图。
(2)$∠MPQ$的度数为$30^{\circ }$或$150^{\circ }$。
(1)如答图。
(2)$∠MPQ$的度数为$30^{\circ }$或$150^{\circ }$。

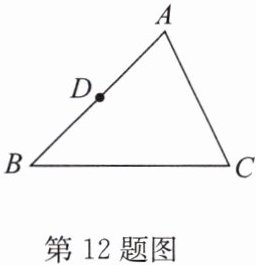
12. 如图,在三角形ABC中,D为AB边的中点.
(1)过点D作线段$DE// BC$交AC于点E;
(2)过点D作线段$DF// AC$交BC于点F;
(3)度量线段AE,CE的长度,度量线段BF,CF的长度,分析这两组数据后,写出你猜想得到的结论;
(4)度量线段DE,BC的长度,度量线段DF,AC的长度,分析这两组数据后,写出你猜想得到的结论.
(1)过点D作线段$DE// BC$交AC于点E;
(2)过点D作线段$DF// AC$交BC于点F;
(3)度量线段AE,CE的长度,度量线段BF,CF的长度,分析这两组数据后,写出你猜想得到的结论;
(4)度量线段DE,BC的长度,度量线段DF,AC的长度,分析这两组数据后,写出你猜想得到的结论.

答案:
(1)如答图,线段 DE 即为所求。
(2)如答图,线段 DF 即为所求。

(3)由度量结果得$AE=CE$,$BF=CF$。
猜想:经过三角形一边的中点,且平行于三角形另一边的直线经过三角形第三边的中点。
(4)由度量结果得$DE=\frac {1}{2}BC$,$DF=\frac {1}{2}AC$。
猜想:连接三角形两边中点的线段的长度等于第三边的一半。
(1)如答图,线段 DE 即为所求。
(2)如答图,线段 DF 即为所求。

(3)由度量结果得$AE=CE$,$BF=CF$。
猜想:经过三角形一边的中点,且平行于三角形另一边的直线经过三角形第三边的中点。
(4)由度量结果得$DE=\frac {1}{2}BC$,$DF=\frac {1}{2}AC$。
猜想:连接三角形两边中点的线段的长度等于第三边的一半。
13. 我们知道同一平面内两条直线的交点个数是0或1,三条直线的交点个数是0或1或2或3.
(1)请你画图说明同一平面内的五条直线最多有几个交点?
(2)同一平面内的五条直线可以有4个交点吗? 如果有,请你画出符合条件的所有图形;如果没有,请说明理由.
(3)在平面内画出10条直线,使交点个数恰好是31.
(1)请你画图说明同一平面内的五条直线最多有几个交点?
(2)同一平面内的五条直线可以有4个交点吗? 如果有,请你画出符合条件的所有图形;如果没有,请说明理由.
(3)在平面内画出10条直线,使交点个数恰好是31.
答案:
(1)如答图①,最多有 10 个交点。

(2)可以有 4 个交点,有 3 种不同的情形,如答图②。

(3)如答图③所示。

(1)如答图①,最多有 10 个交点。

(2)可以有 4 个交点,有 3 种不同的情形,如答图②。

(3)如答图③所示。
