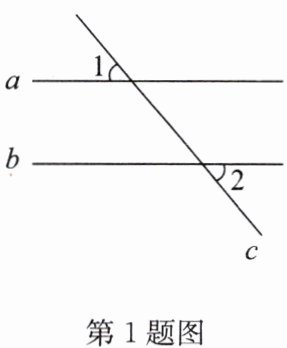
1. 如图,直线a,b被直线c所截,已知$a// b,∠1= 50^{\circ }$,则$∠2$的度数为 (
A.$40^{\circ }$
B.$50^{\circ }$
C.$70^{\circ }$
D.$130^{\circ }$
B
)
A.$40^{\circ }$
B.$50^{\circ }$
C.$70^{\circ }$
D.$130^{\circ }$
答案:B
解析:
∵a//b,∠1=50°
∴∠2=∠1=50°(两直线平行,同位角相等)
答案:B
∴∠2=∠1=50°(两直线平行,同位角相等)
答案:B
2. 如图,直线$AB// CD$,EG平分$∠BEF$,若$∠1= 40^{\circ }$,则$∠2$的度数是 (

A.$70^{\circ }$
B.$50^{\circ }$
C.$40^{\circ }$
D.$140^{\circ }$
A
)
A.$70^{\circ }$
B.$50^{\circ }$
C.$40^{\circ }$
D.$140^{\circ }$
答案:A
解析:
解:∵AB//CD,∠1=40°
∴∠BEF=180°-∠1=140°(两直线平行,同旁内角互补)
∵EG平分∠BEF
∴∠BEG=∠BEF/2=70°
∵AB//CD
∴∠2=∠BEG=70°(两直线平行,内错角相等)
答案:A
∴∠BEF=180°-∠1=140°(两直线平行,同旁内角互补)
∵EG平分∠BEF
∴∠BEG=∠BEF/2=70°
∵AB//CD
∴∠2=∠BEG=70°(两直线平行,内错角相等)
答案:A
3. 如图,$AB// CD$,光线EF从水中射向空气时折射成FH,点G在射线EF上,已知$∠HFB= 20^{\circ },∠FED= 45^{\circ }$,则$∠GFH= $
25
$^{\circ }$.答案:25
解析:
解:因为 $AB // CD$,所以$\angle EFB = \angle FED = 45^{\circ}$(两直线平行,内错角相等)。
又因为$\angle HFB = 20^{\circ}$,所以$\angle GFH=\angle EFB - \angle HFB=45^{\circ}-20^{\circ}=25^{\circ}$。
答案:$25$
又因为$\angle HFB = 20^{\circ}$,所以$\angle GFH=\angle EFB - \angle HFB=45^{\circ}-20^{\circ}=25^{\circ}$。
答案:$25$
4. 如图,$AB// CD// EF$,FC平分$∠AFE,∠C= 25^{\circ }$,则$∠A$的度数是
$50^{\circ}$
.答案:$50^{\circ}$
解析:
解:因为 $CD // EF$,所以 $\angle C = \angle CFE$(两直线平行,内错角相等)。
已知 $\angle C = 25^{\circ}$,则 $\angle CFE = 25^{\circ}$。
因为 $FC$ 平分 $\angle AFE$,所以 $\angle AFE = 2\angle CFE = 2×25^{\circ} = 50^{\circ}$。
因为 $AB // EF$,所以 $\angle A = \angle AFE = 50^{\circ}$(两直线平行,内错角相等)。
故 $\angle A$ 的度数是 $50^{\circ}$。
已知 $\angle C = 25^{\circ}$,则 $\angle CFE = 25^{\circ}$。
因为 $FC$ 平分 $\angle AFE$,所以 $\angle AFE = 2\angle CFE = 2×25^{\circ} = 50^{\circ}$。
因为 $AB // EF$,所以 $\angle A = \angle AFE = 50^{\circ}$(两直线平行,内错角相等)。
故 $\angle A$ 的度数是 $50^{\circ}$。
5. 如图,$AB// CD,AD// BC,∠B与∠D$相等吗?试说明理由.


答案:解:相等.理由:因为 $AB// CD$,所以 $\angle D+\angle A = 180^{\circ}$(两直线平行,同旁内角互补).因为 $AD// BC$,所以 $\angle B+\angle A = 180^{\circ}$(两直线平行,同旁内角互补),所以 $\angle B=\angle D$.
6. 一副三角尺如图所示放置,斜边平行,则$∠1$的度数为 (
A.$5^{\circ }$
B.$10^{\circ }$
C.$15^{\circ }$
D.$20^{\circ }$
C
)A.$5^{\circ }$
B.$10^{\circ }$
C.$15^{\circ }$
D.$20^{\circ }$
答案:C
解析:
解:如图,一副三角尺中,含30°角的三角尺锐角为30°、60°,含45°角的三角尺锐角为45°、45°。
因为两斜边平行,设上面三角尺的60°角顶点为A,下面三角尺的45°角顶点为B,两斜边交点为C。
上面三角尺中,与斜边相邻的内角为60°,其对顶角为60°;下面三角尺中,与斜边相邻的内角为45°,其同位角为45°。
∠1 = 60° - 45° = 15°。
答案:C
因为两斜边平行,设上面三角尺的60°角顶点为A,下面三角尺的45°角顶点为B,两斜边交点为C。
上面三角尺中,与斜边相邻的内角为60°,其对顶角为60°;下面三角尺中,与斜边相邻的内角为45°,其同位角为45°。
∠1 = 60° - 45° = 15°。
答案:C
7. 光线照射到镜面会产生反射现象,由光学知识可知,入射光线与镜面的夹角和反射光线与镜面的夹角相等.如图,一束光线AB先后经平面镜OM,ON反射后,反射光线CD与入射光线AB平行,当$∠ABM= 35^{\circ }$时,$∠DCN$的度数为 (
A.$55^{\circ }$
B.$70^{\circ }$
C.$60^{\circ }$
D.$35^{\circ }$
A
)A.$55^{\circ }$
B.$70^{\circ }$
C.$60^{\circ }$
D.$35^{\circ }$
答案:A
解析:
解:
∵∠ABM=35°,入射光线与镜面夹角等于反射光线与镜面夹角,
∴∠CBM=∠ABM=35°,
∴∠ABC=180°-∠ABM-∠CBM=110°。
∵AB//CD,
∴∠BCD=180°-∠ABC=70°。
设∠DCN=∠OCN=x,则∠BCD=180°-∠OCB-∠OCD=180°-2x=70°,
解得x=55°。
即∠DCN=55°。
A
∵∠ABM=35°,入射光线与镜面夹角等于反射光线与镜面夹角,
∴∠CBM=∠ABM=35°,
∴∠ABC=180°-∠ABM-∠CBM=110°。
∵AB//CD,
∴∠BCD=180°-∠ABC=70°。
设∠DCN=∠OCN=x,则∠BCD=180°-∠OCB-∠OCD=180°-2x=70°,
解得x=55°。
即∠DCN=55°。
A