8. 小明将一块直角三角尺摆放在直尺上,如图所示,则$∠ABC与∠DEF$的关系是 (
A.互余
B.互补
C.同位角
D.同旁内角
A
)A.互余
B.互补
C.同位角
D.同旁内角
答案:A
解析:
解:
∵直尺的两边互相平行,
∴∠ABC与三角尺的另一个锐角相等(两直线平行,同位角相等)。
∵直角三角尺的两个锐角互余,
∴∠ABC与∠DEF互余。
答案:A
∵直尺的两边互相平行,
∴∠ABC与三角尺的另一个锐角相等(两直线平行,同位角相等)。
∵直角三角尺的两个锐角互余,
∴∠ABC与∠DEF互余。
答案:A
9. 如图,把一个长方形纸片沿EF折叠后,点D,C分别落在点$D',C'$处,$∠AED'= 40^{\circ }$,则$∠BFC'= $
$40^{\circ}$
.答案:$40^{\circ}$
解析:
解:
∵四边形ABCD是长方形,
∴AD//BC,∠DEF=∠EFB(两直线平行,内错角相等)。
由折叠性质得:∠D'EF=∠DEF,∠D'=∠D=90°。
∵∠AED'=40°,∠AED'+∠D'EF+∠DEF=180°,
∴∠DEF=(180°-40°)/2=70°,
∴∠EFB=70°。
∵∠D'EF=70°,∠D'=90°,
∴∠D'FE=180°-90°-70°=20°。
∵∠D'FE+∠EFC'=180°(平角定义),
∴∠EFC'=180°-20°=160°。
∵∠EFB+∠BFC'=∠EFC',
∴∠BFC'=∠EFC'-∠EFB=160°-70°=40°。
答案:$40^{\circ}$
∵四边形ABCD是长方形,
∴AD//BC,∠DEF=∠EFB(两直线平行,内错角相等)。
由折叠性质得:∠D'EF=∠DEF,∠D'=∠D=90°。
∵∠AED'=40°,∠AED'+∠D'EF+∠DEF=180°,
∴∠DEF=(180°-40°)/2=70°,
∴∠EFB=70°。
∵∠D'EF=70°,∠D'=90°,
∴∠D'FE=180°-90°-70°=20°。
∵∠D'FE+∠EFC'=180°(平角定义),
∴∠EFC'=180°-20°=160°。
∵∠EFB+∠BFC'=∠EFC',
∴∠BFC'=∠EFC'-∠EFB=160°-70°=40°。
答案:$40^{\circ}$
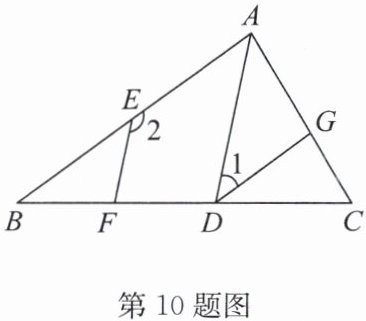
10. 如图,$AB// DG,AD// EF$.
(1)试说明:$∠1+∠2= 180^{\circ };$
(2)若DG是$∠ADC$的平分线,$∠2= 138^{\circ }$,求$∠B$的度数.
(1)试说明:$∠1+∠2= 180^{\circ };$
(2)若DG是$∠ADC$的平分线,$∠2= 138^{\circ }$,求$∠B$的度数.

答案:解:(1)因为 $AD// EF$,所以 $\angle BAD+\angle 2 = 180^{\circ}$.因为 $AB// DG$,所以 $\angle BAD=\angle 1$,所以 $\angle 1+\angle 2 = 180^{\circ}$.(2)因为 $\angle 1+\angle 2 = 180^{\circ}$且 $\angle 2 = 138^{\circ}$,所以 $\angle 1 = 42^{\circ}$.因为 $DG$ 是 $\angle ADC$ 的平分线,所以 $\angle CDG=\angle 1 = 42^{\circ}$.因为 $AB// DG$,所以 $\angle B=\angle CDG = 42^{\circ}$.
11. 如图,点C在$∠AOB$的一边OA上,过点C的直线$DE// OB$,CF平分$∠ACD,CG⊥CF$于点C.
(1)若$∠O= 40^{\circ }$,求$∠ECF$的度数;
(2)试说明:CG平分$∠OCD;$
(3)当$∠O$为多少度时,CD平分$∠OCF$,并说明理由.

(1)若$∠O= 40^{\circ }$,求$∠ECF$的度数;
(2)试说明:CG平分$∠OCD;$
(3)当$∠O$为多少度时,CD平分$∠OCF$,并说明理由.

答案:解:(1)因为 $DE// OB$,所以 $\angle O=\angle ACE$(两直线平行,同位角相等).因为 $\angle O = 40^{\circ}$,所以 $\angle ACE = 40^{\circ}$.因为 $\angle ACD+\angle ACE = 180^{\circ}$(平角的定义),所以 $\angle ACD = 140^{\circ}$.又因为 $CF$ 平分 $\angle ACD$,所以 $\angle ACF = 70^{\circ}$(角平分线的定义),所以 $\angle ECF = 70^{\circ}+40^{\circ}=110^{\circ}$.(2)因为 $CG\perp CF$,所以 $\angle FCG = 90^{\circ}$,所以 $\angle DCG+\angle DCF = 90^{\circ}$.又因为 $\angle ACO = 180^{\circ}$(平角的定义),所以 $\angle GCO+\angle FCA = 90^{\circ}$.因为 $\angle ACF=\angle DCF$,所以 $\angle GCO=\angle GCD$(等角的余角相等),即 $CG$ 平分 $\angle OCD$.(3)结论:当 $\angle O = 60^{\circ}$ 时,$CD$ 平分 $\angle OCF$.理由:当 $\angle O = 60^{\circ}$ 时,因为 $DE// OB$,所以 $\angle DCO=\angle O = 60^{\circ}$(两直线平行,内错角相等),所以 $\angle ACD = 120^{\circ}$.又因为 $CF$ 平分 $\angle ACD$,所以 $\angle DCF = 60^{\circ}$(角平分线的定义),所以 $\angle DCO=\angle DCF$,即 $CD$ 平分 $\angle OCF$.