1.(2024·吴江区期中)如图是小明学习“平行线的性质”时用到的学具,经测量$∠2=105^{\circ }$,要使木条a与b平行,则$∠1$的度数应为(
A.$45^{\circ }$
B.$105^{\circ }$
C.$75^{\circ }$
D.$135^{\circ }$
C
)A.$45^{\circ }$
B.$105^{\circ }$
C.$75^{\circ }$
D.$135^{\circ }$
答案:C
解析:
解:由图可知,∠1与∠2是同旁内角。
因为当a与b平行时,同旁内角互补,
所以∠1 + ∠2 = 180°。
已知∠2 = 105°,
则∠1 = 180° - ∠2 = 180° - 105° = 75°。
答案:C
因为当a与b平行时,同旁内角互补,
所以∠1 + ∠2 = 180°。
已知∠2 = 105°,
则∠1 = 180° - ∠2 = 180° - 105° = 75°。
答案:C
2.如图,直线$l_{1}// l_{2}$,直线$l_{3}$交$l_{1}$于点A,交$l_{2}$于点B,过点B的直线$l_{4}$交$l_{1}$于点C.若$∠3=50^{\circ },∠1+∠2+∠3=240^{\circ }$,则$∠4$的度数是(
A.$80^{\circ }$
B.$70^{\circ }$
C.$60^{\circ }$
D.$50^{\circ }$
B
)A.$80^{\circ }$
B.$70^{\circ }$
C.$60^{\circ }$
D.$50^{\circ }$
答案:B
3.(2024·梁溪区月考)如图,下列条件中,不能判断直线$a// b$的是(
A.$∠1=∠3$
B.$∠2=∠3$
C.$∠4=∠5$
D.$∠2+∠4=180^{\circ }$
B
)A.$∠1=∠3$
B.$∠2=∠3$
C.$∠4=∠5$
D.$∠2+∠4=180^{\circ }$
答案:B
解析:
A. ∠1与∠3是内错角,∠1=∠3时,a//b;
B. ∠2与∠3是同位角,∠2=∠3时,不能判断a//b;
C. ∠4与∠5是同位角,∠4=∠5时,a//b;
D. ∠2与∠4是同旁内角,∠2+∠4=180°时,a//b。
答案:B
B. ∠2与∠3是同位角,∠2=∠3时,不能判断a//b;
C. ∠4与∠5是同位角,∠4=∠5时,a//b;
D. ∠2与∠4是同旁内角,∠2+∠4=180°时,a//b。
答案:B
4.如图,$AB// CD,AC// BD,∠1=28^{\circ }$,则$∠2$的度数为
$28^{\circ}$
.答案:$28^{\circ}$
解析:
解:∵AB//CD,
∴∠1=∠BDC(两直线平行,内错角相等)。
∵AC//BD,
∴∠2=∠BDC(两直线平行,内错角相等)。
∵∠1=28°,
∴∠2=28°。
28°
∴∠1=∠BDC(两直线平行,内错角相等)。
∵AC//BD,
∴∠2=∠BDC(两直线平行,内错角相等)。
∵∠1=28°,
∴∠2=28°。
28°
5.如图,$AB// CD$,直线EF分别交AB,CD于点E,F,EG平分$∠BEF$,若$∠EFG=64^{\circ }$,则$∠EGD$的度数是
$122^{\circ}$
.答案:$122^{\circ}$
解析:
解:
∵AB//CD,
∴∠BEF + ∠EFG = 180°(两直线平行,同旁内角互补)。
∵∠EFG = 64°,
∴∠BEF = 180° - 64° = 116°。
∵EG平分∠BEF,
∴∠BEG = ∠BEF / 2 = 116° / 2 = 58°。
∵AB//CD,
∴∠EGD = 180° - ∠BEG = 180° - 58° = 122°(两直线平行,同旁内角互补)。
122°
∵AB//CD,
∴∠BEF + ∠EFG = 180°(两直线平行,同旁内角互补)。
∵∠EFG = 64°,
∴∠BEF = 180° - 64° = 116°。
∵EG平分∠BEF,
∴∠BEG = ∠BEF / 2 = 116° / 2 = 58°。
∵AB//CD,
∴∠EGD = 180° - ∠BEG = 180° - 58° = 122°(两直线平行,同旁内角互补)。
122°
6.如图,$∠DAF=∠F,∠B=∠D$,AB与DC平行吗?说明理由.请补全推理过程.
解:平行.理由:因为$∠DAF=∠F$(
所以$AD// BF$(
所以$∠D=∠DCF$(
因为$∠B=∠D$(
所以$∠B=∠DCF$(
所以$AB// DC$(
解:平行.理由:因为$∠DAF=∠F$(
已知
),所以$AD// BF$(
内错角相等,两直线平行
),所以$∠D=∠DCF$(
两直线平行,内错角相等
).因为$∠B=∠D$(
已知
),所以$∠B=∠DCF$(
等量代换
),所以$AB// DC$(
同位角相等,两直线平行
).答案:已知 内错角相等,两直线平行 两直线平行,内错角相等 已知 等量代换 同位角相等,两直线平行
解析:
解:平行.理由:因为$∠DAF=∠F$(已知),
所以$AD// BF$(内错角相等,两直线平行),
所以$∠D=∠DCF$(两直线平行,内错角相等).
因为$∠B=∠D$(已知),
所以$∠B=∠DCF$(等量代换),
所以$AB// DC$(同位角相等,两直线平行).
所以$AD// BF$(内错角相等,两直线平行),
所以$∠D=∠DCF$(两直线平行,内错角相等).
因为$∠B=∠D$(已知),
所以$∠B=∠DCF$(等量代换),
所以$AB// DC$(同位角相等,两直线平行).
7.如图,在三角形ABC中,$AH⊥BC$,BF平分$∠ABC,BE⊥BF,EF// BC$,有下列四个结论:①$AH⊥EF$;②$∠ABF=∠EFB$;③$AC// BE$;④$∠E=∠ABE$.其中正确的是(
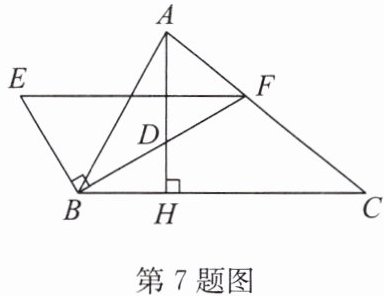
A.①②③④
B.①③
C.①③④
D.①②④
D
)
A.①②③④
B.①③
C.①③④
D.①②④
答案:D
解析:
解:①
∵EF//BC,AH⊥BC,
∴AH⊥EF(两平行线中一条垂直第三条直线,另一条也垂直),①正确。
②
∵BF平分∠ABC,
∴∠ABF=∠FBC。
∵EF//BC,
∴∠EFB=∠FBC(两直线平行,内错角相等),
∴∠ABF=∠EFB,②正确。
③
无法通过已知条件证明AC//BE,③错误。
④
∵BE⊥BF,
∴∠EBF=90°,
∴∠E+∠EFB=90°,∠ABE+∠ABF=90°。
∵∠ABF=∠EFB(已证),
∴∠E=∠ABE,④正确。
综上,正确的是①②④。
答案:D
∵EF//BC,AH⊥BC,
∴AH⊥EF(两平行线中一条垂直第三条直线,另一条也垂直),①正确。
②
∵BF平分∠ABC,
∴∠ABF=∠FBC。
∵EF//BC,
∴∠EFB=∠FBC(两直线平行,内错角相等),
∴∠ABF=∠EFB,②正确。
③
无法通过已知条件证明AC//BE,③错误。
④
∵BE⊥BF,
∴∠EBF=90°,
∴∠E+∠EFB=90°,∠ABE+∠ABF=90°。
∵∠ABF=∠EFB(已证),
∴∠E=∠ABE,④正确。
综上,正确的是①②④。
答案:D