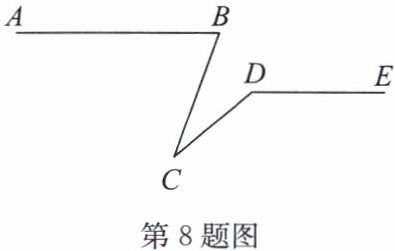
8.如图,$AB// DE,∠ABC=70^{\circ },∠CDE=140^{\circ }$,则$∠BCD$的度数为(
A.$40^{\circ }$
B.$30^{\circ }$
C.$35^{\circ }$
D.$25^{\circ }$
B
) 
A.$40^{\circ }$
B.$30^{\circ }$
C.$35^{\circ }$
D.$25^{\circ }$
答案:B
解析:
解:延长ED交BC于点F。
∵AB//DE,∠ABC=70°,
∴∠BFD=∠ABC=70°(两直线平行,内错角相等)。
∵∠CDE=140°,∠CDE+∠CDF=180°(邻补角定义),
∴∠CDF=180°-140°=40°。
∵∠BFD=∠BCD+∠CDF(三角形外角性质),
∴∠BCD=∠BFD-∠CDF=70°-40°=30°。
答案:B
∵AB//DE,∠ABC=70°,
∴∠BFD=∠ABC=70°(两直线平行,内错角相等)。
∵∠CDE=140°,∠CDE+∠CDF=180°(邻补角定义),
∴∠CDF=180°-140°=40°。
∵∠BFD=∠BCD+∠CDF(三角形外角性质),
∴∠BCD=∠BFD-∠CDF=70°-40°=30°。
答案:B
9.如果两个角的两条边分别平行,且其中一个角比另一个角的3倍少$20^{\circ }$,那么这两个角的度数分别是
$10^{\circ},10^{\circ}$或$130^{\circ},50^{\circ}$
.答案:$10^{\circ},10^{\circ}$或$130^{\circ},50^{\circ}$
解析:
设其中一个角为$x^{\circ}$,则另一个角为$(3x - 20)^{\circ}$。
因为两个角的两条边分别平行,所以这两个角相等或互补。
情况一:两角相等
$x = 3x - 20$
$2x = 20$
$x = 10$
则另一个角为$3×10 - 20 = 10^{\circ}$
情况二:两角互补
$x + (3x - 20) = 180$
$4x - 20 = 180$
$4x = 200$
$x = 50$
则另一个角为$3×50 - 20 = 130^{\circ}$
综上,这两个角的度数分别是$10^{\circ},10^{\circ}$或$130^{\circ},50^{\circ}$。
因为两个角的两条边分别平行,所以这两个角相等或互补。
情况一:两角相等
$x = 3x - 20$
$2x = 20$
$x = 10$
则另一个角为$3×10 - 20 = 10^{\circ}$
情况二:两角互补
$x + (3x - 20) = 180$
$4x - 20 = 180$
$4x = 200$
$x = 50$
则另一个角为$3×50 - 20 = 130^{\circ}$
综上,这两个角的度数分别是$10^{\circ},10^{\circ}$或$130^{\circ},50^{\circ}$。
10.如图,直线$AB// CD$,且被直线MN所截,MN分别交AB和CD于点E,F,点Q在PM上,且$∠EPM=∠FQM$,试说明:$∠DFQ=∠BEP$.


答案:解:因为$∠EPM = ∠FQM$,所以$FQ// EP$(同位角相等,两直线平行),所以$∠MFQ = ∠MEP$(两直线平行,同位角相等)。又因为$AB// CD$,所以$∠MFD = ∠MEB$(两直线平行,同位角相等),所以$∠MFQ - ∠MFD = ∠MEP - ∠MEB$,所以$∠DFQ = ∠BEP$。
11.如图,在三角形ABC中,$CD⊥AB$,垂足为D,点E在BC上,$EF⊥AB$,垂足为F.
(1)CD与EF平行吗?为什么?
(2)如果$∠1=∠2$,且$∠3=100^{\circ }$,求$∠ACB$的度数.
(1)CD与EF平行吗?为什么?
(1)$CD$与$EF$平行。理由如下:因为$CD⊥AB,EF⊥AB$,所以$∠BFE = ∠BDC = 90^{\circ}$,所以$CD// EF$(同位角相等,两直线平行)。
(2)如果$∠1=∠2$,且$∠3=100^{\circ }$,求$∠ACB$的度数.
(2)因为$CD// EF$,所以$∠2 = ∠BCD$(两直线平行,同位角相等)。因为$∠1 = ∠2$,所以$∠BCD = ∠1$(等量代换),所以$DG// BC$(内错角相等,两直线平行),所以$∠ACB = ∠3 = 100^{\circ}$(两直线平行,同位角相等)。
答案:(1)$CD$与$EF$平行。理由如下:因为$CD⊥AB,EF⊥AB$,所以$∠BFE = ∠BDC = 90^{\circ}$,所以$CD// EF$(同位角相等,两直线平行)。(2)因为$CD// EF$,所以$∠2 = ∠BCD$(两直线平行,同位角相等)。因为$∠1 = ∠2$,所以$∠BCD = ∠1$(等量代换),所以$DG// BC$(内错角相等,两直线平行),所以$∠ACB = ∠3 = 100^{\circ}$(两直线平行,同位角相等)。
12.如图,点E,F在直线AB上,点G在线段CD上,ED与FG交于点H,$∠C=∠EFG,∠CED=∠GHD$.
(1)试说明:$CE// GF$;
(2)试判断$∠AED$与$∠D$之间的数量关系,并说明理由;
(3)若$∠EHF=80^{\circ },∠D=30^{\circ }$,求$∠AEM$的度数.

(1)试说明:$CE// GF$;
(2)试判断$∠AED$与$∠D$之间的数量关系,并说明理由;
(3)若$∠EHF=80^{\circ },∠D=30^{\circ }$,求$∠AEM$的度数.

答案:(1)因为$∠CED = ∠GHD$(已知),所以$CE// GF$(同位角相等,两直线平行)。(2)$∠AED + ∠D = 180^{\circ}$。理由如下:因为$CE// GF$,所以$∠C = ∠FGD$(两直线平行,同位角相等)。又因为$∠C = ∠EFG$,所以$∠FGD = ∠EFG$(等量代换),所以$AB// CD$(内错角相等,两直线平行),所以$∠AED + ∠D = 180^{\circ}$(两直线平行,同旁内角互补)。(3)因为$∠GHD = ∠EHF = 80^{\circ},∠D = 30^{\circ}$,所以$∠FGD = 180^{\circ} - 80^{\circ} - 30^{\circ} = 70^{\circ}$。又因为$CE// GF$,所以$∠C = ∠FGD = 70^{\circ}$。又因为$AB// CD$,所以$∠AEC = ∠C = 70^{\circ}$,所以$∠AEM = 180^{\circ} - ∠AEC = 180^{\circ} - 70^{\circ} = 110^{\circ}$。