4. 如图,$ \angle 1 = \angle ACB $,$ \angle 2 = \angle 3 $,$ FH \perp AB $ 于点 $ H $. 那么 $ CD $ 与 $ AB $ 的位置关系如何?请说明理由.
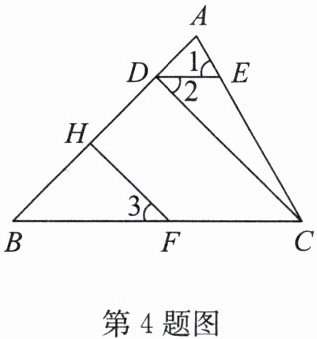

答案:解:$ CD \perp AB $。理由如下:
因为 $ \angle 1 = \angle ACB $,所以 $ DE // BC $,所以 $ \angle 2 = \angle BCD $。
因为 $ \angle 2 = \angle 3 $,所以 $ \angle 3 = \angle BCD $,所以 $ HF // CD $。
因为 $ FH \perp AB $,所以 $ \angle FHB = 90^{\circ} $,
所以 $ \angle CDB = \angle FHB = 90^{\circ} $,
所以 $ CD \perp AB $。
因为 $ \angle 1 = \angle ACB $,所以 $ DE // BC $,所以 $ \angle 2 = \angle BCD $。
因为 $ \angle 2 = \angle 3 $,所以 $ \angle 3 = \angle BCD $,所以 $ HF // CD $。
因为 $ FH \perp AB $,所以 $ \angle FHB = 90^{\circ} $,
所以 $ \angle CDB = \angle FHB = 90^{\circ} $,
所以 $ CD \perp AB $。
5. 如图,$ AB \perp BF $,$ CD \perp BF $,$ \angle 1 = \angle 2 $,试说明:$ \angle 3 = \angle E $.


答案:解:因为 $ AB \perp BF $,$ CD \perp BF $,
所以 $ \angle ABD = \angle CDF = 90^{\circ} $,
所以 $ AB // CD $。
因为 $ \angle 1 = \angle 2 $,
所以 $ AB // EF $,
所以 $ CD // EF $,
所以 $ \angle 3 = \angle E $。
所以 $ \angle ABD = \angle CDF = 90^{\circ} $,
所以 $ AB // CD $。
因为 $ \angle 1 = \angle 2 $,
所以 $ AB // EF $,
所以 $ CD // EF $,
所以 $ \angle 3 = \angle E $。
6. 如图,$ AD $ 既是三角形 $ ABC $ 的高,也是 $ \angle BAC $ 的平分线,点 $ G $ 在线段 $ BD $ 上,过点 $ G $ 作 $ EG \perp BC $,交 $ CA $ 的延长线于点 $ E $,$ \angle E $ 与 $ \angle AFE $ 的度数相等吗?为什么?


答案:解:$ \angle E = \angle AFE $。理由如下:
因为 $ AD $ 既是三角形 $ ABC $ 的高,也是 $ \angle BAC $ 的平分线,
所以 $ AD \perp BC $,$ \angle BAD = \angle CAD $,所以 $ \angle ADC = 90^{\circ} $。
因为 $ EG \perp BC $,所以 $ \angle EGC = 90^{\circ} $,
所以 $ \angle EGC = \angle ADC $,所以 $ AD // EG $,
所以 $ \angle CAD = \angle E $,$ \angle BAD = \angle AFE $,
所以 $ \angle E = \angle AFE $。
因为 $ AD $ 既是三角形 $ ABC $ 的高,也是 $ \angle BAC $ 的平分线,
所以 $ AD \perp BC $,$ \angle BAD = \angle CAD $,所以 $ \angle ADC = 90^{\circ} $。
因为 $ EG \perp BC $,所以 $ \angle EGC = 90^{\circ} $,
所以 $ \angle EGC = \angle ADC $,所以 $ AD // EG $,
所以 $ \angle CAD = \angle E $,$ \angle BAD = \angle AFE $,
所以 $ \angle E = \angle AFE $。