10. 如图,圆的周长为4个单位长度.在该圆的4等分点处分别标上字母A,B,C,D,先把圆周上的点A与数轴上表示数-1的点重合,再将数轴按逆时针方向环绕在该圆上,则数轴上表示数-2025的点与圆周上的点
A
重合.答案：A
解析：
解：圆周长为4个单位长度，4等分点A、B、C、D按逆时针排列。
数轴上-1与A重合，数轴按逆时针环绕圆周，即数轴上数每减小1（向左移动1个单位），对应圆周上点按A→D→C→B→A循环。
计算-1到-2025的距离：$|-1 - (-2025)| = 2024$个单位。
$2024 ÷ 4 = 506$，余数为0。
余数0表示循环完整结束，对应起始点A。
答案：A
数轴上-1与A重合，数轴按逆时针环绕圆周，即数轴上数每减小1（向左移动1个单位），对应圆周上点按A→D→C→B→A循环。
计算-1到-2025的距离：$|-1 - (-2025)| = 2024$个单位。
$2024 ÷ 4 = 506$，余数为0。
余数0表示循环完整结束，对应起始点A。
答案：A
11. 把下列各数填入相应的大括号内:
5.2,0,$\frac{22}{7}$,+(-4),-2$\frac{3}{4}$,-(-3),0.$\dot{2}\dot{5}$.
分数:
非负整数:
负有理数:
5.2,0,$\frac{22}{7}$,+(-4),-2$\frac{3}{4}$,-(-3),0.$\dot{2}\dot{5}$.
分数:
$\{ 5.2,\frac {22}{7},-2\frac {3}{4},0.\dot{2}\dot{5}\}$
;非负整数:
$\{ 0,-(-3)\}$
;负有理数:
$\{ +(-4),-2\frac {3}{4}\}$
.答案：解:分数:$\{ 5.2,\frac {22}{7},-2\frac {3}{4},0.2\dot {5}\} ;$非负整数:$\{ 0,-(-3)\} ;$负有理数:$\{ +(-4),-2\frac {3}{4}\} .$
12. 在数轴上表示下列各数,并用“＜”号将这些数连接起来.
-(-5),-|2|,-1$\frac{1}{2}$,0.5,-(-3),-|-4|,3.5.
-(-5),-|2|,-1$\frac{1}{2}$,0.5,-(-3),-|-4|,3.5.
答案：
解:如答图.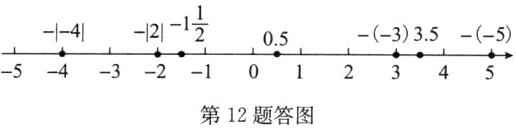
用“＜”号连接起来为$-|-4|＜-|2|＜-1\frac {1}{2}＜0.5＜-(-3)＜3.5＜-(-5).$
解:如答图.
用“＜”号连接起来为$-|-4|＜-|2|＜-1\frac {1}{2}＜0.5＜-(-3)＜3.5＜-(-5).$13. 超市、书店、玩具店依次坐落在一条东西走向的大街上,超市在书店西边20米处,玩具店在书店东边50米处.小明从书店出来沿街向东走了50米,接着又向东走了-80米,此时小明的位置在何处?在数轴上标出超市、书店、玩具店的位置以及小明最后的位置.
答案：
解:以向东为正方向，书店为原点画数轴，1个单位长度表示10米，由于小明从书店出来沿街向东走了50米，接着又向东走了 -80米，小明最后的位置在书店西边30米处，如答图.
解:以向东为正方向，书店为原点画数轴，1个单位长度表示10米，由于小明从书店出来沿街向东走了50米，接着又向东走了 -80米，小明最后的位置在书店西边30米处，如答图.
14. 某厂生产闹钟,检验时,比标准时间多的记为正数,比标准时间少的记为负数,检验结果如下表:
(1)指出哪台闹钟的时间最准确;
(2)规定误差不超过5s的为合格品,否则为次品,则合格的闹钟有几台?
(1)指出哪台闹钟的时间最准确;
(2)规定误差不超过5s的为合格品,否则为次品,则合格的闹钟有几台?
答案：解:(1)由题意，得1~5号数据的绝对值分别为2,3.5，6,7,4,因为$2＜3.5＜4＜6＜7$，所以1号闹钟的时间最准确.(2)由(1)知绝对值不大于5的有2,3.5,4，故合格的闹钟有3台.