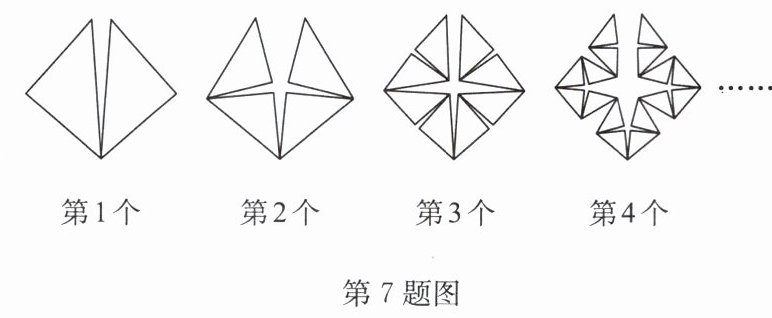
7. 分形的概念是由数学家本华·曼德博提出的. 如图是分形的一种, 第 1 个图案有 2 个三角形;第 2 个图案有 4 个三角形; 第 3 个图案有 8 个三角形; 第 4 个图案有 16 个三角形, $\cdots$, 下列数据中是按此规律分形得到的三角形的个数的是 (
A.126
B.513
C.980
D.1024
D
)
A.126
B.513
C.980
D.1024
答案:D
解析:
观察图案可知,第1个图案有2个三角形,第2个图案有4个三角形,第3个图案有8个三角形,第4个图案有16个三角形,规律为第n个图案中三角形的个数是$2^n$。
A. $2^n=126$,n不是整数,不符合规律;
B. $2^n=513$,n不是整数,不符合规律;
C. $2^n=980$,n不是整数,不符合规律;
D. $2^{10}=1024$,符合规律。
答案:D
A. $2^n=126$,n不是整数,不符合规律;
B. $2^n=513$,n不是整数,不符合规律;
C. $2^n=980$,n不是整数,不符合规律;
D. $2^{10}=1024$,符合规律。
答案:D
8. 如图, 将形状、大小完全相同的“•”和线段按照一定规律摆成图形, 第 1 个图形中“•”的个数为 3 , 第 2 个图形中“•”的个数为 8 , 第 3 个图形中“•”的个数为 15 , $\cdots$, 依此类推, 第 $n$ 个图形中“•”的个数为
$n(n + 2)$
.答案:$n(n + 2)$
解析:
解:第1个图形中“•”的个数为$3=1×3$,
第2个图形中“•”的个数为$8=2×4$,
第3个图形中“•”的个数为$15=3×5$,
观察可得规律:第$n$个图形中“•”的个数为$n(n+2)$。
$n(n + 2)$
第2个图形中“•”的个数为$8=2×4$,
第3个图形中“•”的个数为$15=3×5$,
观察可得规律:第$n$个图形中“•”的个数为$n(n+2)$。
$n(n + 2)$
9. (2024·建邺区开学) 按如图所示的方法搭 1 个三角形需要 3 根小棒, 搭 2 个三角形需要 5 根小棒, 那么搭 10 个三角形需要

21
根小棒, 搭 $n$ 个三角形需要$(2n + 1)$
根小棒.
答案:21 $(2n + 1)$
解析:
搭1个三角形需要3根小棒,可表示为$2×1 + 1$;搭2个三角形需要5根小棒,可表示为$2×2 + 1$;搭3个三角形需要7根小棒,可表示为$2×3 + 1$。
则搭10个三角形需要小棒:$2×10 + 1 = 21$(根)
搭$n$个三角形需要小棒:$(2n + 1)$根
21;$(2n + 1)$
则搭10个三角形需要小棒:$2×10 + 1 = 21$(根)
搭$n$个三角形需要小棒:$(2n + 1)$根
21;$(2n + 1)$
10. 如图(1)是由若干个小圆圈堆成的一个形如等边三角形的图案, 最上面一层有一个圆圈, 以下各层均比上一层多一个圆圈, 一共堆了 $n$ 层. 将图(1)倒置后与原图(1)拼成图(2)的形状, 这样我们可以算出图(1)中所有圆圈的个数为 $1+2+3+\cdots+n=\frac{n(n+1)}{2}$. 如果图(3), 图(4)中的圆圈共有 13 层, 请解答下列问题:
(1)如图(3), 我们自上往下, 在每个圆圈中填上一串连续的正整数 $1,2,3,4, \cdots$, 则最底层最左边的圆圈中的数是____
(2)如图(4), 我们自上往下, 在每个圆圈中填上一串连续的整数 $-23,-22,-21,-20, \cdots$, 则最底层最右边的圆圈中的数是____
(3)求图(4)中所有圆圈中各数的绝对值之和. (写出计算过程)
解: 题图④中共有 91 个数, 其中 23 个负数, 1 个 0, 67 个正数,
所以题图④中所有圆圈中各数的绝对值之和为
$\vert - 23\vert + \vert - 22\vert + \cdots + \vert - 1\vert + 0 + 1 + 2 + \cdots + 67$
$= (1 + 2 + 3 + \cdots + 23) + (1 + 2 + 3 + \cdots + 67)$
$= 276 + 2278$
$= 2554$.
(1)如图(3), 我们自上往下, 在每个圆圈中填上一串连续的正整数 $1,2,3,4, \cdots$, 则最底层最左边的圆圈中的数是____
79
;(2)如图(4), 我们自上往下, 在每个圆圈中填上一串连续的整数 $-23,-22,-21,-20, \cdots$, 则最底层最右边的圆圈中的数是____
67
;(3)求图(4)中所有圆圈中各数的绝对值之和. (写出计算过程)
解: 题图④中共有 91 个数, 其中 23 个负数, 1 个 0, 67 个正数,
所以题图④中所有圆圈中各数的绝对值之和为
$\vert - 23\vert + \vert - 22\vert + \cdots + \vert - 1\vert + 0 + 1 + 2 + \cdots + 67$
$= (1 + 2 + 3 + \cdots + 23) + (1 + 2 + 3 + \cdots + 67)$
$= 276 + 2278$
$= 2554$.
答案:(1) 79 (2) 67
(3) 解: 题图④中共有 91 个数, 其中 23 个负数, 1 个 0, 67 个正数,
所以题图④中所有圆圈中各数的绝对值之和为
$\vert - 23\vert + \vert - 22\vert + \cdots + \vert - 1\vert + 0 + 1 + 2 + \cdots + 67$
$= (1 + 2 + 3 + \cdots + 23) + (1 + 2 + 3 + \cdots + 67)$
$= 276 + 2278$
$= 2554$.
(3) 解: 题图④中共有 91 个数, 其中 23 个负数, 1 个 0, 67 个正数,
所以题图④中所有圆圈中各数的绝对值之和为
$\vert - 23\vert + \vert - 22\vert + \cdots + \vert - 1\vert + 0 + 1 + 2 + \cdots + 67$
$= (1 + 2 + 3 + \cdots + 23) + (1 + 2 + 3 + \cdots + 67)$
$= 276 + 2278$
$= 2554$.