1. 当 $ a = - 2 $ 时,代数式 $ a ^ { 2 } - 2 a $ 的值是(
A.$ - 8 $
B.$ - 4 $
C.$ 8 $
D.$ 4 $
C
)A.$ - 8 $
B.$ - 4 $
C.$ 8 $
D.$ 4 $
答案:C
解析:
当$a = -2$时,
$a^2 - 2a = (-2)^2 - 2×(-2)$
$= 4 + 4$
$= 8$
答案:C
$a^2 - 2a = (-2)^2 - 2×(-2)$
$= 4 + 4$
$= 8$
答案:C
2. 按照如图所示的运算程序进行运算,若输入 $ x $ 的值为 $ - 3 $,则输出 $ y $ 的值为
-4
.答案:-4
解析:
解:
输入 $ x = -3 $
第一步:$ -3 + 2 = -1 $
第二步:$ (-1)^2 = 1 $
第三步:$ 1 - 5 = -4 $
输出 $ y = -4 $
输入 $ x = -3 $
第一步:$ -3 + 2 = -1 $
第二步:$ (-1)^2 = 1 $
第三步:$ 1 - 5 = -4 $
输出 $ y = -4 $
3. (1)若 $ x = 1 $,则 $ 3 x - 2 = $
(2)若 $ a ^ { 2 } - 3 b = 1 $,则 $ 2 a ^ { 2 } - 6 b + 2025 = $
(3)已知 $ \frac { x - 3 y } { 2 x + y } = - 6 $,那么 $ \frac { 2 x + y } { x - 3 y } $ 的值为
1
;(2)若 $ a ^ { 2 } - 3 b = 1 $,则 $ 2 a ^ { 2 } - 6 b + 2025 = $
2027
;(3)已知 $ \frac { x - 3 y } { 2 x + y } = - 6 $,那么 $ \frac { 2 x + y } { x - 3 y } $ 的值为
$-\frac{1}{6}$
,$ \frac { 2 x - 6 y } { 2 x + y } $ 的值为-12
.答案:(1)1 (2)2027 (3)$-\frac{1}{6}$ -12
解析:
(1)当$x = 1$时,$3x - 2 = 3×1 - 2 = 1$;
(2)因为$a^2 - 3b = 1$,所以$2a^2 - 6b = 2(a^2 - 3b) = 2×1 = 2$,则$2a^2 - 6b + 2025 = 2 + 2025 = 2027$;
(3)因为$\frac{x - 3y}{2x + y} = -6$,所以$\frac{2x + y}{x - 3y} = -\frac{1}{6}$;$\frac{2x - 6y}{2x + y} = 2×\frac{x - 3y}{2x + y} = 2×(-6) = -12$。
(2)因为$a^2 - 3b = 1$,所以$2a^2 - 6b = 2(a^2 - 3b) = 2×1 = 2$,则$2a^2 - 6b + 2025 = 2 + 2025 = 2027$;
(3)因为$\frac{x - 3y}{2x + y} = -6$,所以$\frac{2x + y}{x - 3y} = -\frac{1}{6}$;$\frac{2x - 6y}{2x + y} = 2×\frac{x - 3y}{2x + y} = 2×(-6) = -12$。
4. 已知一个三角形的底边长为 $ a $,底边上的高为 $ h $,则它的面积 $ S = $
$\frac{1}{2}ah$
. 若 $ S = 8 $,$ h = 5 $,则 $ a = $3.2
.答案:$\frac{1}{2}ah$ 3.2
5. 当 $ a = - 1 $,$ b = - 3 $,$ c = 5 $ 时,求下列各代数式的值:
(1)$ b ^ { 2 } - 4 a c $;
(2)$ ( a + b - c ) ^ { 2 } $.
(1)$ b ^ { 2 } - 4 a c $;
(2)$ ( a + b - c ) ^ { 2 } $.
答案:解:(1)当$a=-1$,$b=-3$,$c=5$时,
$b^{2}-4ac=(-3)^{2}-4×(-1)×5=9+20=29$。
(2)当$a=-1$,$b=-3$,$c=5$时,
$(a+b-c)^{2}=(-1-3-5)^{2}=81$。
$b^{2}-4ac=(-3)^{2}-4×(-1)×5=9+20=29$。
(2)当$a=-1$,$b=-3$,$c=5$时,
$(a+b-c)^{2}=(-1-3-5)^{2}=81$。
6. (2024·鼓楼区三模)如果 $ a - b + 3 = 0 $,那么代数式 $ 1 - 2 a + 2 b $ 的值是(
A.$ - 5 $
B.$ - 7 $
C.$ 4 $
D.$ 7 $
D
)A.$ - 5 $
B.$ - 7 $
C.$ 4 $
D.$ 7 $
答案:D
解析:
解:由 $a - b + 3 = 0$,得 $a - b = -3$。
$1 - 2a + 2b = 1 - 2(a - b)$
将 $a - b = -3$ 代入上式,得:
$1 - 2×(-3) = 1 + 6 = 7$
答案:D
$1 - 2a + 2b = 1 - 2(a - b)$
将 $a - b = -3$ 代入上式,得:
$1 - 2×(-3) = 1 + 6 = 7$
答案:D
7. 不论 $ a $ 取什么值,下列代数式的值总是正数的是(
A.$ | a + 1 | $
B.$ | a | + 1 $
C.$ a ^ { 2 } $
D.$ ( a + 1 ) ^ { 2 } $
B
)A.$ | a + 1 | $
B.$ | a | + 1 $
C.$ a ^ { 2 } $
D.$ ( a + 1 ) ^ { 2 } $
答案:B
解析:
解:
A. 当$a=-1$时,$|a + 1|=| - 1+1|=0$,不是正数;
B. 因为$|a|\geq0$,所以$|a| + 1\geq1$,总是正数;
C. 当$a=0$时,$a^{2}=0$,不是正数;
D. 当$a=-1$时,$(a + 1)^{2}=(-1 + 1)^{2}=0$,不是正数。
故选:B
A. 当$a=-1$时,$|a + 1|=| - 1+1|=0$,不是正数;
B. 因为$|a|\geq0$,所以$|a| + 1\geq1$,总是正数;
C. 当$a=0$时,$a^{2}=0$,不是正数;
D. 当$a=-1$时,$(a + 1)^{2}=(-1 + 1)^{2}=0$,不是正数。
故选:B
8. 当 $ x = 1 $ 时,代数式 $ a x ^ { 3 } + b x - 2 $ 的值为 $ 2 $,则当 $ x = - 1 $ 时,该代数式的值是(
A.$ - 6 $
B.$ - 2 $
C.$ 0 $
D.$ 2 $
A
)A.$ - 6 $
B.$ - 2 $
C.$ 0 $
D.$ 2 $
答案:A
解析:
解:当$x = 1$时,$a×1^3 + b×1 - 2 = 2$,即$a + b - 2 = 2$,所以$a + b = 4$。
当$x = -1$时,代数式为$a×(-1)^3 + b×(-1) - 2 = -a - b - 2 = -(a + b) - 2$。
将$a + b = 4$代入,得$-4 - 2 = -6$。
A
当$x = -1$时,代数式为$a×(-1)^3 + b×(-1) - 2 = -a - b - 2 = -(a + b) - 2$。
将$a + b = 4$代入,得$-4 - 2 = -6$。
A
9. 按如图所示的运算程序进行运算,则当输入 $ x $ 的值为
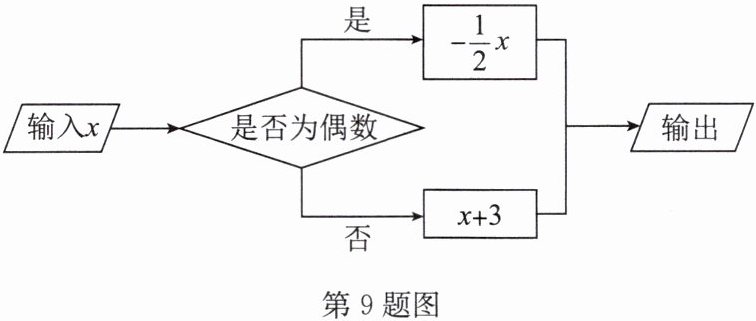
5 或 -16
时,输出的结果为 $ 8 $.
答案:5 或 -16
解析:
当输入的$x$为奇数时,输出结果为$x + 3$,令$x + 3=8$,解得$x = 5$,5是奇数,符合条件;
当输入的$x$为偶数时,输出结果为$-\frac{1}{2}x$,令$-\frac{1}{2}x=8$,解得$x=-16$,-16是偶数,符合条件。
5 或 -16
当输入的$x$为偶数时,输出结果为$-\frac{1}{2}x$,令$-\frac{1}{2}x=8$,解得$x=-16$,-16是偶数,符合条件。
5 或 -16