10. 如图所示的每个图形中的四个数都是按相同的规律填写的,根据此规律确定代数式 $ m n - x $ 的值为
-180
.答案:-180
解析:
观察图形规律:
左上角数字依次为1,2,3,4,...,第n个图形左上角为n;
左下角数字依次为2,4,6,8,...,第n个图形左下角为2n;
右上角数字依次为1,3,5,7,...,第n个图形右上角为2n-1;
右下角数字:1=1×2-1,10=2×4+2,27=3×6+9,52=4×8+20,规律为右下角=左上角×左下角+右上角×(n-1),即x=n×2n+(2n-1)(n-1)。
当左下角为20时,2n=20,得n=10。
则m=2n-1=19,x=10×20+19×9=200+171=371。
mn-x=10×19-371=190-371=-180。
-180
左上角数字依次为1,2,3,4,...,第n个图形左上角为n;
左下角数字依次为2,4,6,8,...,第n个图形左下角为2n;
右上角数字依次为1,3,5,7,...,第n个图形右上角为2n-1;
右下角数字:1=1×2-1,10=2×4+2,27=3×6+9,52=4×8+20,规律为右下角=左上角×左下角+右上角×(n-1),即x=n×2n+(2n-1)(n-1)。
当左下角为20时,2n=20,得n=10。
则m=2n-1=19,x=10×20+19×9=200+171=371。
mn-x=10×19-371=190-371=-180。
-180
11. 如图,某长方形广场的长为 $ a \mathrm { ~m } $,宽为 $ b \mathrm { ~m } $,中间有一个圆形花坛,半径为 $ c \mathrm { ~m } $.
(1)用代数式表示图中阴影部分的面积;
(2)若 $ a = 100 $,$ b = 50 $,$ c = 10 $,求阴影部分的面积.($ \pi $ 取 $ 3.14 $)
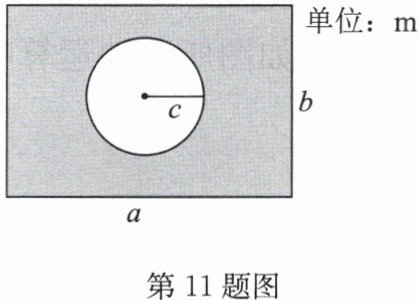
(1)用代数式表示图中阴影部分的面积;
(2)若 $ a = 100 $,$ b = 50 $,$ c = 10 $,求阴影部分的面积.($ \pi $ 取 $ 3.14 $)

答案:解:(1)$S_{阴影}=(ab-πc^{2})m^{2}$。
(2)当$a=100$,$b=50$,$c=10$时,
$S_{阴影}=ab-πc^{2}=100×50-3.14×10^{2}=5000-314=4686(m^{2})$。
(2)当$a=100$,$b=50$,$c=10$时,
$S_{阴影}=ab-πc^{2}=100×50-3.14×10^{2}=5000-314=4686(m^{2})$。
12. 观察下列表格中两个代数式及其相应的值,回答问题:

【初步感知】
(1)根据表中信息可知:$ a = $
【归纳规律】
(2)表中 $ - 2 x + 5 $ 的值的变化规律是:$ x $ 的值每增加 $ 1 $,$ - 2 x + 5 $ 的值就减少 $ 2 $. 类似地,$ 2 x - 7 $ 的值的变化规律是:
【问题解决】
(3)请直接写出一个含 $ x $ 的代数式,要求 $ x $ 的值每增加 $ 1 $,代数式的值就减小 $ 5 $,且当 $ x = 0 $ 时,代数式的值为 $ - 7 $.

【初步感知】
(1)根据表中信息可知:$ a = $
1
;$ b = $-3
;【归纳规律】
(2)表中 $ - 2 x + 5 $ 的值的变化规律是:$ x $ 的值每增加 $ 1 $,$ - 2 x + 5 $ 的值就减少 $ 2 $. 类似地,$ 2 x - 7 $ 的值的变化规律是:
$x$的值每增加 $1$,$2x - 7$ 的值就增加 $2$
;【问题解决】
(3)请直接写出一个含 $ x $ 的代数式,要求 $ x $ 的值每增加 $ 1 $,代数式的值就减小 $ 5 $,且当 $ x = 0 $ 时,代数式的值为 $ - 7 $.
$-5x - 7$
答案:(1)1 -3 (2)$x$的值每增加 $1$,$2x - 7$ 的值就增加 $2$ (3)解:这个含 $x$ 的代数式是 $-5x - 7$。
解析:
(1)1;-3
(2)$x$的值每增加1,$2x-7$的值就增加2
(3)$-5x-7$
(2)$x$的值每增加1,$2x-7$的值就增加2
(3)$-5x-7$
13. 已知代数式 $ ( m + n ) ^ { 2 } $ 和 $ m ^ { 2 } + 2 m n + n ^ { 2 } $.
(1)当 $ m = 2 $,$ n = 1 $ 时,求这两个代数式的值;
(2)写出这两个代数式的值的关系;
(3)当 $ m = 4 $,$ n = - 2 $ 时,(2)中的结论是否仍成立?
(4)根据(2)中的结论,你能用简便方法算出当 $ m = 0.125 $,$ n = 0.875 $ 时,$ m ^ { 2 } + 2 m n + n ^ { 2 } $ 的值吗?
(1)当 $ m = 2 $,$ n = 1 $ 时,求这两个代数式的值;
(2)写出这两个代数式的值的关系;
(3)当 $ m = 4 $,$ n = - 2 $ 时,(2)中的结论是否仍成立?
(4)根据(2)中的结论,你能用简便方法算出当 $ m = 0.125 $,$ n = 0.875 $ 时,$ m ^ { 2 } + 2 m n + n ^ { 2 } $ 的值吗?
答案:解:(1)当$m = 2$,$n = 1$ 时,$(m + n)^2=(2 + 1)^2=9$,
$m^2 + 2mn + n^2=2^2 + 2×2×1 + 1^2=9$。
(2)$(m + n)^2=m^2 + 2mn + n^2$。
(3)当$m = 4$,$n = -2$ 时,$(m + n)^2=[4 + (-2)]^2=2^2=4$,
$m^2 + 2mn + n^2=4^2 + 2×4×(-2)+(-2)^2=16 + (-16)+4=4$,
所以$(m + n)^2=m^2 + 2mn + n^2$仍成立。
(4)根据(2)中的结论,得$m^2 + 2mn + n^2=(m + n)^2$。
当$m = 0.125$,$n = 0.875$ 时,
$m^2 + 2mn + n^2=(m + n)^2=(0.125 + 0.875)^2=1$。
$m^2 + 2mn + n^2=2^2 + 2×2×1 + 1^2=9$。
(2)$(m + n)^2=m^2 + 2mn + n^2$。
(3)当$m = 4$,$n = -2$ 时,$(m + n)^2=[4 + (-2)]^2=2^2=4$,
$m^2 + 2mn + n^2=4^2 + 2×4×(-2)+(-2)^2=16 + (-16)+4=4$,
所以$(m + n)^2=m^2 + 2mn + n^2$仍成立。
(4)根据(2)中的结论,得$m^2 + 2mn + n^2=(m + n)^2$。
当$m = 0.125$,$n = 0.875$ 时,
$m^2 + 2mn + n^2=(m + n)^2=(0.125 + 0.875)^2=1$。