11. (1)写出下列各单项式的系数和次数:
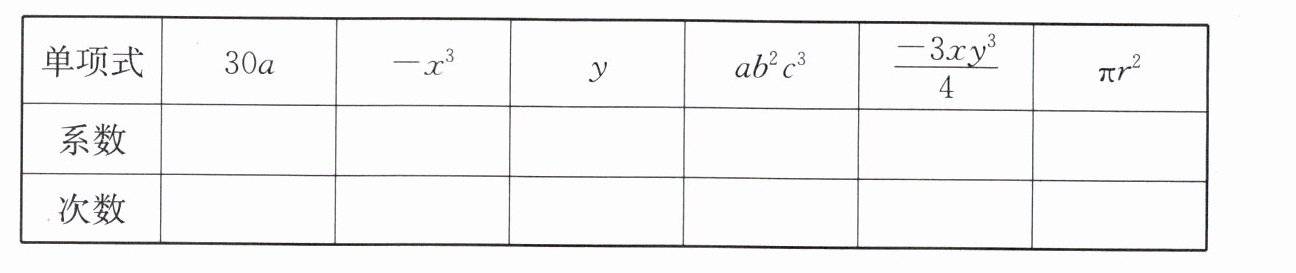
(2)写出下列各多项式的项和次数:


(2)写出下列各多项式的项和次数:

答案:
解:(1)
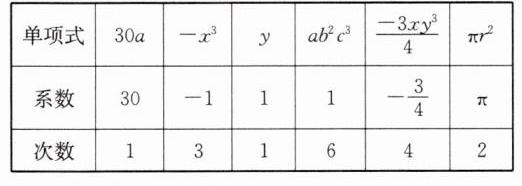
(2)

解:(1)

(2)

12. 已知关于$x的整式(|k| - 3)x^{3}+(k - 3)x^{2}-kx$。
(1)若此整式是单项式,求$k$的值;
(2)若此整式是二次多项式,求$k$的值。
(1)若此整式是单项式,求$k$的值;
(2)若此整式是二次多项式,求$k$的值。
答案:解:(1)因为关于 x 的整式是单项式,
所以$|k|-3 = 0$且$k - 3 = 0$,解得$k = 3$,所以 k 的值是 3.
(2)因为关于 x 的整式是二次多项式,所以$|k|-3 = 0$且$k - 3 \neq 0$,解得$k = -3$,
所以 k 的值是 -3.
所以$|k|-3 = 0$且$k - 3 = 0$,解得$k = 3$,所以 k 的值是 3.
(2)因为关于 x 的整式是二次多项式,所以$|k|-3 = 0$且$k - 3 \neq 0$,解得$k = -3$,
所以 k 的值是 -3.
13. 小明在抄写单项式时,把有的字母中的指数漏掉了,抄成了$-\frac{4}{5}xyz$,他只知道这个单项式是四次单项式,你能帮他写出这个单项式吗?这样的单项式有几个,不妨都写出来。
答案:解:这个单项式可能是$-\frac {4}{5}x^{2}yz$或$-\frac {4}{5}xy^{2}z$或$-\frac {4}{5}xyz^{2}.$
解析:
解:因为原单项式是四次单项式,小明抄成了$-\frac{4}{5}xyz$,此时$x$、$y$、$z$的指数均为$1$,指数和为$1 + 1+ 1=3$,所以漏掉的指数之和为$4-3 = 1$,即需要在$x$、$y$、$z$的指数中恰有一个指数增加$1$。
这样的单项式有$3$个,分别是:
$-\frac{4}{5}x^{2}yz$;
$-\frac{4}{5}xy^{2}z$;
$-\frac{4}{5}xyz^{2}$。
这样的单项式有$3$个,分别是:
$-\frac{4}{5}x^{2}yz$;
$-\frac{4}{5}xy^{2}z$;
$-\frac{4}{5}xyz^{2}$。
14. 定义:$f(a,b)是关于a,b$的多项式,如果$f(a,b)= f(b,a)$,那么$f(a,b)$叫作“对称多项式”。例如,如果$f(a,b)= a^{2}+a + b + b^{2}$,那么$f(b,a)= b^{2}+b + a + a^{2}$,显然$f(a,b)= f(b,a)$,所以$f(a,b)$是“对称多项式”。
(1)试说明:$f(a,b)= a^{2}-2ab + b^{2}$是“对称多项式”;
(2)请写出一个“对称多项式”,$f(a,b)= $
(3)如果$f_{1}(a,b)和f_{2}(a,b)$均为“对称多项式”,那么$f_{1}(a,b)+f_{2}(a,b)$一定是“对称多项式”吗?如果是,说明理由;如果不是,举例说明。
(1)试说明:$f(a,b)= a^{2}-2ab + b^{2}$是“对称多项式”;
(2)请写出一个“对称多项式”,$f(a,b)= $
$a + b$
;(不多于四项)(3)如果$f_{1}(a,b)和f_{2}(a,b)$均为“对称多项式”,那么$f_{1}(a,b)+f_{2}(a,b)$一定是“对称多项式”吗?如果是,说明理由;如果不是,举例说明。
(1)解:因为$f(a,b)=a^{2}-2ab + b^{2}$,所以$f(b,a)=b^{2}-2ba + a^{2},$
显然$f(a,b)=f(b,a)$,所以$f(a,b)=a^{2}-2ab + b^{2}$是“对称多项式”.
(3)解:不一定.当$f_{1}(a,b)=a + b,f_{2}(a,b)=-a - b$时,
$f_{1}(a,b)+f_{2}(a,b)=0$,此时$f_{1}(a,b)+f_{2}(a,b)$是单项式,不是多项式.
显然$f(a,b)=f(b,a)$,所以$f(a,b)=a^{2}-2ab + b^{2}$是“对称多项式”.
(3)解:不一定.当$f_{1}(a,b)=a + b,f_{2}(a,b)=-a - b$时,
$f_{1}(a,b)+f_{2}(a,b)=0$,此时$f_{1}(a,b)+f_{2}(a,b)$是单项式,不是多项式.
答案:(1)解:因为$f(a,b)=a^{2}-2ab + b^{2}$,所以$f(b,a)=b^{2}-2ba + a^{2},$
显然$f(a,b)=f(b,a)$,所以$f(a,b)=a^{2}-2ab + b^{2}$是“对称多项式”.
(2)$a + b$(答案不唯一)
(3)解:不一定.当$f_{1}(a,b)=a + b,f_{2}(a,b)=-a - b$时,
$f_{1}(a,b)+f_{2}(a,b)=0$,此时$f_{1}(a,b)+f_{2}(a,b)$是单项式,不是多项式.
显然$f(a,b)=f(b,a)$,所以$f(a,b)=a^{2}-2ab + b^{2}$是“对称多项式”.
(2)$a + b$(答案不唯一)
(3)解:不一定.当$f_{1}(a,b)=a + b,f_{2}(a,b)=-a - b$时,
$f_{1}(a,b)+f_{2}(a,b)=0$,此时$f_{1}(a,b)+f_{2}(a,b)$是单项式,不是多项式.