10. 有一道题目是一个多项式减去$x^{2}+14x - 6$,小强误当成了加法计算,结果得到$2x^{2}-x + 3$,则正确的结果是
$-29x + 15$
.答案:$ -29x + 15 $
解析:
解:设这个多项式为$A$。
因为小强误当成加法计算,所以$A + (x^{2}+14x - 6)=2x^{2}-x + 3$
则$A=(2x^{2}-x + 3)-(x^{2}+14x - 6)$
$=2x^{2}-x + 3 - x^{2}-14x + 6$
$=x^{2}-15x + 9$
正确结果应为$A-(x^{2}+14x - 6)=(x^{2}-15x + 9)-(x^{2}+14x - 6)$
$=x^{2}-15x + 9 - x^{2}-14x + 6$
$=-29x + 15$
$-29x + 15$
因为小强误当成加法计算,所以$A + (x^{2}+14x - 6)=2x^{2}-x + 3$
则$A=(2x^{2}-x + 3)-(x^{2}+14x - 6)$
$=2x^{2}-x + 3 - x^{2}-14x + 6$
$=x^{2}-15x + 9$
正确结果应为$A-(x^{2}+14x - 6)=(x^{2}-15x + 9)-(x^{2}+14x - 6)$
$=x^{2}-15x + 9 - x^{2}-14x + 6$
$=-29x + 15$
$-29x + 15$
11. 若关于$a$,$b的多项式3(a^{2}-2ab - b^{2})-(a^{2}+mab + 2b^{2})$中不含有ab项,则$m = $
-6
.答案:$-6$
解析:
解:原式$=3a^{2}-6ab - 3b^{2}-a^{2}-mab - 2b^{2}$
$=(3a^{2}-a^{2})+(-6ab - mab)+(-3b^{2}-2b^{2})$
$=2a^{2}+(-6 - m)ab - 5b^{2}$
因为多项式中不含有$ab$项,所以$-6 - m=0$,解得$m=-6$。
$-6$
$=(3a^{2}-a^{2})+(-6ab - mab)+(-3b^{2}-2b^{2})$
$=2a^{2}+(-6 - m)ab - 5b^{2}$
因为多项式中不含有$ab$项,所以$-6 - m=0$,解得$m=-6$。
$-6$
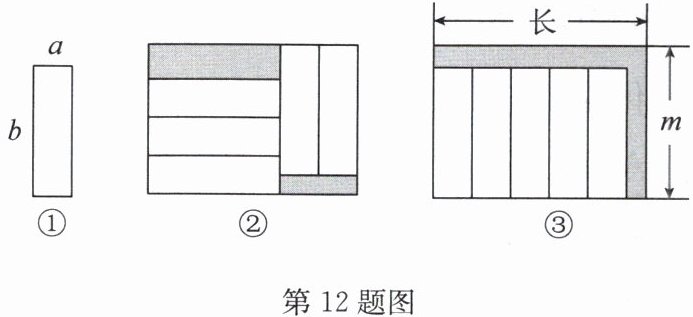
12. 如图,把五个长为$b$,宽为$a$的小长方形,按图②和图③两种方式放在一个宽为$m$的大长方形上(相邻的小长方形既无重叠,又不留空隙).设图②中两块阴影部分的周长和为$C_{1}$,图③中阴影部分的周长为$C_{2}$,若大长方形的长比宽大$(5 - a)$,则$C_{2}-C_{1}$的值为______
10
.
答案:$ 10 $
解析:
解:由图②,大长方形宽$m = b$,上面阴影长方形周长为$2(a + m)$,下面阴影长方形周长为$2[(b - 2a) + m]$,则$C_{1}=2(a + m)+2[(b - 2a)+m]=2b + 4m$。
由图③,大长方形宽$m = 5a$,阴影部分周长$C_{2}=2(\text{长}+m)$,且长$=m + 5 - a$,故$C_{2}=2(m + 5 - a + m)=4m + 10 - 2a$。
因为$m = b$且$m = 5a$,所以$b = 5a$。
$C_{2}-C_{1}=(4m + 10 - 2a)-(2b + 4m)=10 - 2a - 2b$,将$b = 5a$代入得$10 - 2a - 10a=10 - 12a + 12a=10$。
答案:$10$
由图③,大长方形宽$m = 5a$,阴影部分周长$C_{2}=2(\text{长}+m)$,且长$=m + 5 - a$,故$C_{2}=2(m + 5 - a + m)=4m + 10 - 2a$。
因为$m = b$且$m = 5a$,所以$b = 5a$。
$C_{2}-C_{1}=(4m + 10 - 2a)-(2b + 4m)=10 - 2a - 2b$,将$b = 5a$代入得$10 - 2a - 10a=10 - 12a + 12a=10$。
答案:$10$
13. 计算:
(1) $-2x-[x^{2}-2(x^{2}-3x)]$; (2) $7a^{2}b-[4ab - 3(ab-\frac{7}{3}a^{2}b)+ab]$.
(1) $-2x-[x^{2}-2(x^{2}-3x)]$; (2) $7a^{2}b-[4ab - 3(ab-\frac{7}{3}a^{2}b)+ab]$.
答案:解:(1)原式$ = -2x - (x^{2} - 2x^{2} + 6x) = -2x - (-x^{2} + 6x) = -2x + x^{2} - 6x = x^{2} - 8x $。
(2)原式$ = 7a^{2}b - (4ab - 3ab + 7a^{2}b + ab) = 7a^{2}b - 7a^{2}b - 2ab = -2ab $。
(2)原式$ = 7a^{2}b - (4ab - 3ab + 7a^{2}b + ab) = 7a^{2}b - 7a^{2}b - 2ab = -2ab $。
14. (1) 已知$x= \frac{1}{2}$,求$(2x^{2}-\frac{1}{2}+3x)-4(x - x^{2}+\frac{1}{2})$的值;
(2) 先化简,再求值:$2a^{2}-[\frac{1}{2}(4a^{2}-ab)+8ab]-\frac{1}{2}ab$,其中$a = 1$,$b= \frac{1}{4}$.
(2) 先化简,再求值:$2a^{2}-[\frac{1}{2}(4a^{2}-ab)+8ab]-\frac{1}{2}ab$,其中$a = 1$,$b= \frac{1}{4}$.
答案:解:(1)原式$ = 2x^{2} - \frac{1}{2} + 3x - 4x + 4x^{2} - 2 = 6x^{2} - x - \frac{5}{2} $。
因为$ x = \frac{1}{2} $,所以原式$ = 6×\frac{1}{4} - \frac{1}{2} - \frac{5}{2} = -\frac{3}{2} $。
(2)原式$ = 2a^{2} - (2a^{2} - \frac{1}{2}ab + 8ab) - \frac{1}{2}ab = 2a^{2} - 2a^{2} + \frac{1}{2}ab - 8ab - \frac{1}{2}ab = -8ab $。
当$ a = 1 $,$ b = \frac{1}{4} $时,原式$ = -8×1×\frac{1}{4} = -2 $。
因为$ x = \frac{1}{2} $,所以原式$ = 6×\frac{1}{4} - \frac{1}{2} - \frac{5}{2} = -\frac{3}{2} $。
(2)原式$ = 2a^{2} - (2a^{2} - \frac{1}{2}ab + 8ab) - \frac{1}{2}ab = 2a^{2} - 2a^{2} + \frac{1}{2}ab - 8ab - \frac{1}{2}ab = -8ab $。
当$ a = 1 $,$ b = \frac{1}{4} $时,原式$ = -8×1×\frac{1}{4} = -2 $。
15. 已知多项式$(2x^{2}+ax - y + 6)-(bx^{2}-2x + 5y - 1)$.
(1) 若多项式的值与字母$x$的取值无关,求$a$,$b$的值;
(2) 在(1)的条件下,先化简多项式$2(a^{2}-ab + b^{2})-(a^{2}+ab + 2b^{2})$,再求它的值.
(1) 若多项式的值与字母$x$的取值无关,求$a$,$b$的值;
(2) 在(1)的条件下,先化简多项式$2(a^{2}-ab + b^{2})-(a^{2}+ab + 2b^{2})$,再求它的值.
答案:解:(1)$ (2x^{2} + ax - y + 6)-(bx^{2}-2x + 5y - 1) $
$ = 2x^{2} + ax - y + 6 - bx^{2} + 2x - 5y + 1 $
$ = (2 - b)x^{2} + (a + 2)x - 6y + 7 $。
因为多项式的值与字母$ x $的取值无关,
所以$ a + 2 = 0 $,$ 2 - b = 0 $,
所以$ a = -2 $,$ b = 2 $。
(2)$ 2(a^{2}-ab + b^{2})-(a^{2}+ab + 2b^{2}) $
$ = 2a^{2} - 2ab + 2b^{2} - a^{2} - ab - 2b^{2} $
$ = a^{2} - 3ab $,
当$ a = -2 $,$ b = 2 $时,原式$ = 4 + 12 = 16 $。
$ = 2x^{2} + ax - y + 6 - bx^{2} + 2x - 5y + 1 $
$ = (2 - b)x^{2} + (a + 2)x - 6y + 7 $。
因为多项式的值与字母$ x $的取值无关,
所以$ a + 2 = 0 $,$ 2 - b = 0 $,
所以$ a = -2 $,$ b = 2 $。
(2)$ 2(a^{2}-ab + b^{2})-(a^{2}+ab + 2b^{2}) $
$ = 2a^{2} - 2ab + 2b^{2} - a^{2} - ab - 2b^{2} $
$ = a^{2} - 3ab $,
当$ a = -2 $,$ b = 2 $时,原式$ = 4 + 12 = 16 $。
16. 已知$A = 3a^{2}b - 2ab^{2}+abc$,小明错将“$2A - B$”看成“$2A + B$”,算得结果$C = 4a^{2}b - 3ab^{2}+4abc$.
(1) 求$B$;
(2) 求$2A - B$的正确结果;
(3) 小强说(2)中的结果的大小与$c$的取值无关,对吗?若$a= \frac{1}{8}$,$b= \frac{1}{5}$,求(2)中代数式的值.
(1) 求$B$;
(2) 求$2A - B$的正确结果;
(3) 小强说(2)中的结果的大小与$c$的取值无关,对吗?若$a= \frac{1}{8}$,$b= \frac{1}{5}$,求(2)中代数式的值.
答案:解:(1)因为$ 2A + B = C $,
所以$ B = C - 2A $
$ = 4a^{2}b - 3ab^{2} + 4abc - 2(3a^{2}b - 2ab^{2} + abc) $
$ = 4a^{2}b - 3ab^{2} + 4abc - 6a^{2}b + 4ab^{2} - 2abc $
$ = -2a^{2}b + ab^{2} + 2abc $。
(2)$ 2A - B = 2(3a^{2}b - 2ab^{2} + abc) - (-2a^{2}b + ab^{2} + 2abc) $
$ = 6a^{2}b - 4ab^{2} + 2abc + 2a^{2}b - ab^{2} - 2abc $
$ = 8a^{2}b - 5ab^{2} $。
(3)小强说得对,$ 2A - B $与$ c $的取值无关。
将$ a = \frac{1}{8} $,$ b = \frac{1}{5} $代入,得
$ 8a^{2}b - 5ab^{2} = 8×(\frac{1}{8})^{2}×\frac{1}{5} - 5×\frac{1}{8}×(\frac{1}{5})^{2} = 0 $。
所以$ B = C - 2A $
$ = 4a^{2}b - 3ab^{2} + 4abc - 2(3a^{2}b - 2ab^{2} + abc) $
$ = 4a^{2}b - 3ab^{2} + 4abc - 6a^{2}b + 4ab^{2} - 2abc $
$ = -2a^{2}b + ab^{2} + 2abc $。
(2)$ 2A - B = 2(3a^{2}b - 2ab^{2} + abc) - (-2a^{2}b + ab^{2} + 2abc) $
$ = 6a^{2}b - 4ab^{2} + 2abc + 2a^{2}b - ab^{2} - 2abc $
$ = 8a^{2}b - 5ab^{2} $。
(3)小强说得对,$ 2A - B $与$ c $的取值无关。
将$ a = \frac{1}{8} $,$ b = \frac{1}{5} $代入,得
$ 8a^{2}b - 5ab^{2} = 8×(\frac{1}{8})^{2}×\frac{1}{5} - 5×\frac{1}{8}×(\frac{1}{5})^{2} = 0 $。