7. 已知 $ a ^ { 2 } - a - 5 = 0 $,求 $ ( 3 a ^ { 2 } - 7 a ) - 2 ( a ^ { 2 } - 3 a + 2 ) $ 的值。
答案:解:原式$=3a^{2}-7a-2a^{2}+6a-4=a^{2}-a-4$。因为$a^{2}-a-5=0$,所以$a^{2}-a=5$,所以原式$=5-4=1$。
8. 已知当 $ x = - 1 $ 时,代数式 $ a x ^ { 3 } + b x + 1 $ 的值为 $ - 2025 $,当 $ x = 1 $ 时,求代数式 $ a x ^ { 3 } + b x + 1 $ 的值。
答案:解:当$x=-1$时,$ax^{3}+bx+1=-a-b+1=-2025$,所以$a+b=2026$。当$x=1$时,$ax^{3}+bx+1=a+b+1=2026+1=2027$。
解析:
解:当$x = -1$时,$ax^{3}+bx + 1 = a(-1)^{3}+b(-1)+1=-a - b + 1$,已知此时值为$-2025$,则$-a - b + 1=-2025$,移项可得$-a - b=-2026$,两边同时乘以$-1$得$a + b=2026$。
当$x = 1$时,$ax^{3}+bx + 1 = a(1)^{3}+b(1)+1=a + b + 1$,将$a + b=2026$代入,得$2026+1=2027$。
故当$x = 1$时,代数式的值为$2027$。
当$x = 1$时,$ax^{3}+bx + 1 = a(1)^{3}+b(1)+1=a + b + 1$,将$a + b=2026$代入,得$2026+1=2027$。
故当$x = 1$时,代数式的值为$2027$。
9. 已知 $ 3 x ^ { 2 } - 4 x y = 31 $,$ 4 x y - 3 y ^ { 2 } = 35 $,求代数式 $ x ^ { 2 } - y ^ { 2 } $ 的值。
答案:解:因为$(3x^{2}-4xy)+(4xy-3y^{2})=31+35=66$,即$3x^{2}-3y^{2}=66$,所以$x^{2}-y^{2}=22$。
解析:
解:已知$3x^{2}-4xy = 31$,$4xy - 3y^{2}=35$,
将两式相加得:$(3x^{2}-4xy)+(4xy - 3y^{2})=31 + 35$,
即$3x^{2}-3y^{2}=66$,
两边同时除以$3$得:$x^{2}-y^{2}=22$。
故代数式$x^{2}-y^{2}$的值为$22$。
将两式相加得:$(3x^{2}-4xy)+(4xy - 3y^{2})=31 + 35$,
即$3x^{2}-3y^{2}=66$,
两边同时除以$3$得:$x^{2}-y^{2}=22$。
故代数式$x^{2}-y^{2}$的值为$22$。
10. 已知 $ x ^ { 2 } - x y = - 3 $,$ 2 x y - y ^ { 2 } = - 8 $,求代数式 $ 2 x ^ { 2 } + 4 x y - 3 y ^ { 2 } $ 的值。
答案:解:原式$=2x^{2}-2xy+6xy-3y^{2}=2(x^{2}-xy)+3(2xy-y^{2})=2×(-3)+3×(-8)=-30$。
解析:
解:原式$=2x^{2}-2xy+6xy-3y^{2}$
$=2(x^{2}-xy)+3(2xy-y^{2})$
因为$x^{2}-xy=-3$,$2xy-y^{2}=-8$
所以原式$=2×(-3)+3×(-8)$
$=-6-24$
$=-30$
$=2(x^{2}-xy)+3(2xy-y^{2})$
因为$x^{2}-xy=-3$,$2xy-y^{2}=-8$
所以原式$=2×(-3)+3×(-8)$
$=-6-24$
$=-30$
11. 根据如图所示的程序计算,若输入 $ x $ 的值为 $ - 1 $,则输出 $ y $ 的值为多少?
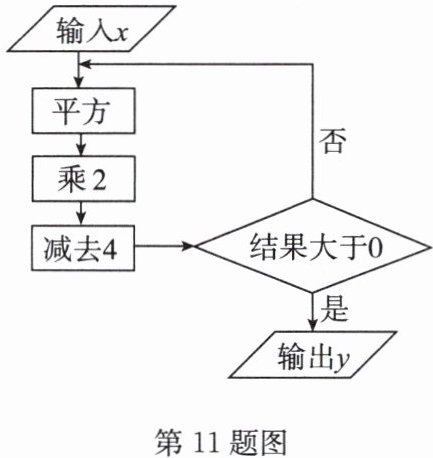

答案:解:由题意可知当$2x^{2}-4>0$时,$y=2x^{2}-4$。若输入$x$的值为$-1$,则$2x^{2}-4=2×(-1)^{2}-4=2-4=-2$,$-2<0$,再输入$x=-2$,则$2x^{2}-4=2×(-2)^{2}-4=8-4=4$,$4>0$,所以$y=4$,即输出$y$的值为4。
解析:
解:输入$x=-1$,计算$2x^{2}-4=2×(-1)^{2}-4=2 - 4=-2$,$-2<0$;
再输入$x=-2$,计算$2x^{2}-4=2×(-2)^{2}-4=8 - 4=4$,$4>0$,
所以输出$y$的值为$4$。
答:输出$y$的值为$4$。
再输入$x=-2$,计算$2x^{2}-4=2×(-2)^{2}-4=8 - 4=4$,$4>0$,
所以输出$y$的值为$4$。
答:输出$y$的值为$4$。