9. 某课外活动小组中女生人数占全组人数的一半,如果再增加6名女生,那么女生人数就占全组人数的$\frac{2}{3}$.求这个课外活动小组的人数.
答案:解:设这个课外活动小组的人数为 x,根据题意,得 $\frac{1}{2}x + 6 = \frac{2}{3}(x + 6)$,解得 x = 12.答:这个课外活动小组的人数为 12.
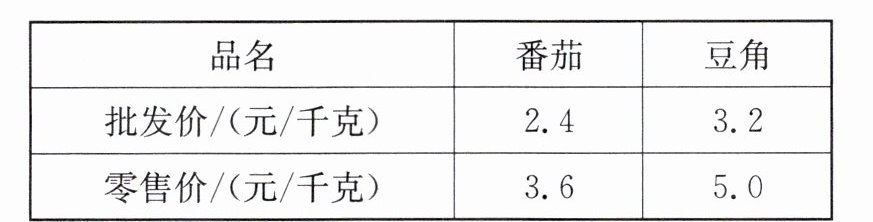
10. 某蔬菜经营户用120元从蔬菜市场批发了番茄和豆角共45千克,番茄、豆角当天的批发价、零售价如下表:
(1)这天该经营户批发了番茄和豆角各多少千克?
(2)当天卖完这些番茄和豆角能盈利多少元?

(1)这天该经营户批发了番茄和豆角各多少千克?
(2)当天卖完这些番茄和豆角能盈利多少元?
答案:(1)解:设这天该经营户批发了番茄 x 千克,豆角(45 - x)千克,根据题意,得 2.4x + 3.2(45 - x) = 120,解得 x = 30,所以 45 - x = 45 - 30 = 15.答:这天该经营户批发了番茄 30 千克,豆角 15 千克.(2)(3.6 - 2.4)×30 + (5.0 - 3.2)×15 = 63(元).答:当天卖完这些番茄和豆角能盈利 63 元.
11. 现用21张纸板制作盒子,每张纸板可制作盒身(侧面)2个或盒底3个,一个盒身配两个盒底.
(1)为不浪费纸板,若设用x张纸板制作盒身,剩下的纸板制作盒底,使得盒身与盒底刚好配套,列出方程并求解出x;
(2)若有63张同样的纸板,一共可制作多少个盒子?
(1)为不浪费纸板,若设用x张纸板制作盒身,剩下的纸板制作盒底,使得盒身与盒底刚好配套,列出方程并求解出x;
(2)若有63张同样的纸板,一共可制作多少个盒子?
答案:(1)解:设用 x 张纸板制作盒身,则用(21 - x)张纸板制作盒底,根据题意,得 $2x = \frac{3(21 - x)}{2}$,解得 x = 9.(2)由(1)可知 21 张纸板可以制作 2×9 = 18(个)盒子,所以 63 张同样的纸板可以制作盒子的个数为 63÷21×18 = 54.答:一共可制作 54 个盒子.
12. 在纸盒制作的劳动实践课上,对规格是$150cm×120cm$的原材料板材进行裁剪得到A型长方形纸板和B型正方形纸板.为了避免材料浪费,每张原材料板材先裁得4张$150cm×30cm$的纸板条,每张纸板条又恰好可以裁得3张A型长方形纸板或5张B型正方形纸板,如图①所示.(单位:cm)
(1)每张原材料板材可以裁得A型纸板
(2)现有130张原材料板材全部裁剪(每张原材料板材只能用一种裁法)得到A型与B型纸板当侧面和底面,做成如图②所示的竖式有盖长方体纸盒(1个长方体纸盒需要4个侧面和2个底面,接缝忽略不计).问:怎样裁剪才能使剪出的A,B型纸板恰好用完?能做多少个纸盒?

(1)每张原材料板材可以裁得A型纸板
12
张或裁得B型纸板20
张;(2)现有130张原材料板材全部裁剪(每张原材料板材只能用一种裁法)得到A型与B型纸板当侧面和底面,做成如图②所示的竖式有盖长方体纸盒(1个长方体纸盒需要4个侧面和2个底面,接缝忽略不计).问:怎样裁剪才能使剪出的A,B型纸板恰好用完?能做多少个纸盒?

解:设用 x 张原材料板材裁剪 A 型纸板,则用(130 - x)张原材料板材裁剪 B 型纸板,根据题意,得 $\frac{12x}{4} = \frac{20(130 - x)}{2}$,解得 x = 100,所以 130 - x = 130 - 100 = 30,$\frac{12x}{4} = \frac{12×100}{4} = 300$.答:用 100 张原材料板材裁剪 A 型纸板,30 张原材料板材裁剪 B 型纸板才能使剪出的 A,B 型纸板恰好用完,能做 300 个纸盒.
答案:(1)12 20(2)解:设用 x 张原材料板材裁剪 A 型纸板,则用(130 - x)张原材料板材裁剪 B 型纸板,根据题意,得 $\frac{12x}{4} = \frac{20(130 - x)}{2}$,解得 x = 100,所以 130 - x = 130 - 100 = 30,$\frac{12x}{4} = \frac{12×100}{4} = 300$.答:用 100 张原材料板材裁剪 A 型纸板,30 张原材料板材裁剪 B 型纸板才能使剪出的 A,B 型纸板恰好用完,能做 300 个纸盒.