21. (12分)已知一块直角三角形纸板的两直角边长分别为6 cm和8 cm.
(1)将直角三角形纸板绕三角形的边所在的直线旋转一周,能得到
(2)绕三角形的直角边所在的直线旋转一周,计算得到的几何体的体积.(圆锥的体积$V= \frac {1}{3}πr^{2}h$,其中π取3)
(1)将直角三角形纸板绕三角形的边所在的直线旋转一周,能得到
3
种大小不同的几何体;(2)绕三角形的直角边所在的直线旋转一周,计算得到的几何体的体积.(圆锥的体积$V= \frac {1}{3}πr^{2}h$,其中π取3)
解: $ \frac { 1 } { 3 } × 3 × 6 ^ { 2 } × 8 = 288 ( \mathrm { cm } ^ { 3 } ) $ 或 $ \frac { 1 } { 3 } × 3 × 8 ^ { 2 } × 6 = 384 ( \mathrm { cm } ^ { 3 } ) $.
故得到的几何体的体积为 $ 288 \mathrm { cm } ^ { 3 } $ 或 $ 384 \mathrm { cm } ^ { 3 } $.
故得到的几何体的体积为 $ 288 \mathrm { cm } ^ { 3 } $ 或 $ 384 \mathrm { cm } ^ { 3 } $.
答案:(1)3
(2)解: $ \frac { 1 } { 3 } × 3 × 6 ^ { 2 } × 8 = 288 ( \mathrm { cm } ^ { 3 } ) $ 或 $ \frac { 1 } { 3 } × 3 × 8 ^ { 2 } × 6 = 384 ( \mathrm { cm } ^ { 3 } ) $.
故得到的几何体的体积为 $ 288 \mathrm { cm } ^ { 3 } $ 或 $ 384 \mathrm { cm } ^ { 3 } $.
(2)解: $ \frac { 1 } { 3 } × 3 × 6 ^ { 2 } × 8 = 288 ( \mathrm { cm } ^ { 3 } ) $ 或 $ \frac { 1 } { 3 } × 3 × 8 ^ { 2 } × 6 = 384 ( \mathrm { cm } ^ { 3 } ) $.
故得到的几何体的体积为 $ 288 \mathrm { cm } ^ { 3 } $ 或 $ 384 \mathrm { cm } ^ { 3 } $.
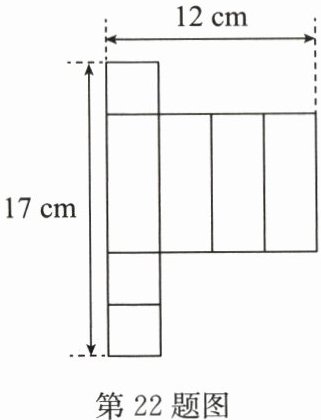
22. (12分)数学课上,老师让同学们用若干个正方形和长方形拼成一个长方体的展开图.拼完后,小明看来看去觉得所拼图形似乎存在问题.
(1)请你帮小明分析一下拼图是否存在问题,若有多余块,则把图中多余块涂上阴影;若还缺少,则直接在原图中补全;
(2)长方体共有______条棱,若将一个长方体沿某些棱剪开并展开成(1)中修正后的平面图形,需要剪开______条棱;
(3)根据图中的数据,求出修正后的展开图所折叠而成的长方体的体积.
(1)请你帮小明分析一下拼图是否存在问题,若有多余块,则把图中多余块涂上阴影;若还缺少,则直接在原图中补全;
(2)长方体共有______条棱,若将一个长方体沿某些棱剪开并展开成(1)中修正后的平面图形,需要剪开______条棱;
(3)根据图中的数据,求出修正后的展开图所折叠而成的长方体的体积.

答案:
(1)解:有多余块,如答图.
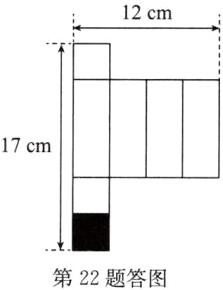
(2)12 7
(3)解:底面正方形的边长为 $ 12 ÷ 4 = 3 ( \mathrm { cm } ) $,
长方体的高为 $ 17 - 3 × 3 = 8 ( \mathrm { cm } ) $,
长方体的体积为 $ 3 × 3 × 8 = 72 ( \mathrm { cm } ^ { 3 } ) $.
答:修正后的展开图所折叠而成的长方体的体积为 $ 72 \mathrm { cm } ^ { 3 } $.
(1)解:有多余块,如答图.

(2)12 7
(3)解:底面正方形的边长为 $ 12 ÷ 4 = 3 ( \mathrm { cm } ) $,
长方体的高为 $ 17 - 3 × 3 = 8 ( \mathrm { cm } ) $,
长方体的体积为 $ 3 × 3 × 8 = 72 ( \mathrm { cm } ^ { 3 } ) $.
答:修正后的展开图所折叠而成的长方体的体积为 $ 72 \mathrm { cm } ^ { 3 } $.
23. (12分)如图,水平桌面上有甲、乙、丙三个圆柱形容器,并在距离容器底部30 cm处用两根相同的管子连接,其中甲、丙两容器的底面积均为$80cm^{2}$,乙容器的底面积为$320cm^{2}$,甲容器中有水$480cm^{3}$.现同时向乙、丙两个容器内匀速注水,直至每个容器都注满水时停止注水,已知每个容器每分钟注水$1600cm^{3}$.
(1)当甲、乙两个容器中水的高度第一次相等时,求注水的时间;
(2)当甲、乙两个容器中水的高度相差3 cm时,求注水的时间.

(1)当甲、乙两个容器中水的高度第一次相等时,求注水的时间;
(2)当甲、乙两个容器中水的高度相差3 cm时,求注水的时间.

答案:解:(1)$ 480 ÷ 80 = 6 ( \mathrm { cm } ) $,
$ 6 × 320 ÷ 1600 = 1.2 ( \mathrm { min } ) $.
答:注水时间为 $ 1.2 \mathrm { min } $.
(2)①当乙容器中的水还未到达管子连接处时,
因为甲、乙两个容器中水的高度相差 3 cm,甲容器中水的高度为 6 cm,
所以乙容器中水的高度为 3 cm 或 9 cm,
当乙容器中水的高度为 3 cm 时,
$ 3 × 320 ÷ 1600 = 0.6 ( \mathrm { min } ) $.
当乙容器中水的高度为 9 cm 时,丙容器中的水到达管子连接处所需时间为 $ 30 × 80 ÷ 1600 = 1.5 ( \mathrm { min } ) $,
$ 1.5 × 1600 ÷ 320 = 7.5 ( \mathrm { cm } ) $,
$ ( 9 - 7.5 ) × 320 ÷ ( 1600 × 2 ) = 0.15 ( \mathrm { min } ) $,
$ 1.5 + 0.15 = 1.65 ( \mathrm { min } ) $.
②当乙容器中的水到达管子连接处后,
因为甲、乙两个容器中水的高度相差 3 cm,
所以此时甲容器水的高度是 27 cm,
$ ( 30 - 7.5 ) × 320 ÷ ( 1600 × 2 ) = 2.25 ( \mathrm { min } ) $,
$ ( 27 - 6 ) × 80 ÷ ( 1600 × 2 ) = 0.525 ( \mathrm { min } ) $,
$ 1.5 + 2.25 + 0.525 = 4.275 ( \mathrm { min } ) $.
答:注水的时间为 $ 0.6 \mathrm { min } $, $ 1.65 \mathrm { min } $, $ 4.275 \mathrm { min } $.
$ 6 × 320 ÷ 1600 = 1.2 ( \mathrm { min } ) $.
答:注水时间为 $ 1.2 \mathrm { min } $.
(2)①当乙容器中的水还未到达管子连接处时,
因为甲、乙两个容器中水的高度相差 3 cm,甲容器中水的高度为 6 cm,
所以乙容器中水的高度为 3 cm 或 9 cm,
当乙容器中水的高度为 3 cm 时,
$ 3 × 320 ÷ 1600 = 0.6 ( \mathrm { min } ) $.
当乙容器中水的高度为 9 cm 时,丙容器中的水到达管子连接处所需时间为 $ 30 × 80 ÷ 1600 = 1.5 ( \mathrm { min } ) $,
$ 1.5 × 1600 ÷ 320 = 7.5 ( \mathrm { cm } ) $,
$ ( 9 - 7.5 ) × 320 ÷ ( 1600 × 2 ) = 0.15 ( \mathrm { min } ) $,
$ 1.5 + 0.15 = 1.65 ( \mathrm { min } ) $.
②当乙容器中的水到达管子连接处后,
因为甲、乙两个容器中水的高度相差 3 cm,
所以此时甲容器水的高度是 27 cm,
$ ( 30 - 7.5 ) × 320 ÷ ( 1600 × 2 ) = 2.25 ( \mathrm { min } ) $,
$ ( 27 - 6 ) × 80 ÷ ( 1600 × 2 ) = 0.525 ( \mathrm { min } ) $,
$ 1.5 + 2.25 + 0.525 = 4.275 ( \mathrm { min } ) $.
答:注水的时间为 $ 0.6 \mathrm { min } $, $ 1.65 \mathrm { min } $, $ 4.275 \mathrm { min } $.