23. (8分)如图,在三角形$ABC$中,$AD平分\angle BAC$,$E为边AB$上一点,连接$DE$,$\angle EAD= \angle EDA$. 试说明:$DE// AC$.


答案:解:因为AD平分∠BAC,
所以∠BAD = ∠CAD.
因为∠EAD = ∠EDA,
所以∠CAD = ∠EDA,
所以DE // AC.
所以∠BAD = ∠CAD.
因为∠EAD = ∠EDA,
所以∠CAD = ∠EDA,
所以DE // AC.
24. (10分)如图,$C是线段AB$上一点,$AB= 12\mathrm{cm}$,$AC= 4\mathrm{cm}$,$P$,$Q两点分别同时从点A$,$C出发以1\mathrm{cm}/\mathrm{s}$,$2\mathrm{cm}/\mathrm{s}的速度沿直线AB$向右运动,运动的时间为$t\mathrm{s}$.
(1)当$t= 1$时,$CP=$
(2)当$t$的值为多少时,$PQ= \frac{1}{2}AB$?
(3)当$t$的值为多少时,$BQ= AP$?
(1)当$t= 1$时,$CP=$
3
$\mathrm{cm}$,$QB=$6
$\mathrm{cm}$;(2)当$t$的值为多少时,$PQ= \frac{1}{2}AB$?
解:t s后,AP = t cm,AQ = (4 + 2t)cm,所以(4 + 2t) - t = $\frac{1}{2}$×12,解得t = 2.故当t = 2时,PQ = $\frac{1}{2}$AB.
(3)当$t$的值为多少时,$BQ= AP$?
解:t s后,AP = t cm,BQ = |8 - 2t| cm,所以t = |8 - 2t|,解得t = 8或t = $\frac{8}{3}$.故当t = 8或t = $\frac{8}{3}$时,BQ = AP.
答案:(1) 3 6
(2)解:t s后,AP = t cm,AQ = (4 + 2t)cm,
所以(4 + 2t) - t = $\frac{1}{2}$×12,解得t = 2.
故当t = 2时,PQ = $\frac{1}{2}$AB.
(3)解:t s后,AP = t cm,BQ = |8 - 2t| cm,所以t = |8 - 2t|,解得t = 8或t = $\frac{8}{3}$.
故当t = 8或t = $\frac{8}{3}$时,BQ = AP.
(2)解:t s后,AP = t cm,AQ = (4 + 2t)cm,
所以(4 + 2t) - t = $\frac{1}{2}$×12,解得t = 2.
故当t = 2时,PQ = $\frac{1}{2}$AB.
(3)解:t s后,AP = t cm,BQ = |8 - 2t| cm,所以t = |8 - 2t|,解得t = 8或t = $\frac{8}{3}$.
故当t = 8或t = $\frac{8}{3}$时,BQ = AP.
25. (12分)已知$\angle AOD= 160^{\circ}$,$OB为\angle AOD$内部的一条射线.
(1)如图①,若$OM平分\angle AOB$,$ON平分\angle BOD$,则$\angle MON$的度数为______;
(2)如图②,$\angle BOC在\angle AOD$内部($\angle AOC>\angle AOB$),且$\angle BOC= 20^{\circ}$,$OF平分\angle AOC$,$OG平分\angle BOD$(射线$OG在射线OC$左侧),求$\angle FOG$的度数;
(3)在(2)的条件下,$\angle BOC绕点O$运动过程中,若$\angle BOF= 8^{\circ}$,求$\angle COG$的度数.

(1)如图①,若$OM平分\angle AOB$,$ON平分\angle BOD$,则$\angle MON$的度数为______;
(2)如图②,$\angle BOC在\angle AOD$内部($\angle AOC>\angle AOB$),且$\angle BOC= 20^{\circ}$,$OF平分\angle AOC$,$OG平分\angle BOD$(射线$OG在射线OC$左侧),求$\angle FOG$的度数;
(3)在(2)的条件下,$\angle BOC绕点O$运动过程中,若$\angle BOF= 8^{\circ}$,求$\angle COG$的度数.

答案:
(1) 80°
(2)解:因为OF平分∠AOC,OG平分∠BOD,
所以∠FOC = $\frac{1}{2}$∠AOC,∠BOG = $\frac{1}{2}$∠BOD,
所以∠FOG = ∠FOC + ∠BOG - ∠BOC = $\frac{1}{2}$∠AOC + $\frac{1}{2}$∠BOD - ∠BOC = $\frac{1}{2}$(∠AOC + ∠BOD) - ∠BOC = $\frac{1}{2}$(∠AOD + ∠BOC) - ∠BOC = $\frac{1}{2}$(∠AOD - ∠BOC) = $\frac{1}{2}$×(160° - 20°) = 70°.
(3)解:当OF在OB的右侧时,如题图②.
设∠COG = x,则∠BOG = x + 20°.
因为OF平分∠AOC,OG平分∠BOD,
所以∠AOF = ∠FOC = 20° + 8° = 28°,∠BOD = 2(x + 20°).
因为∠AOD = ∠AOF + ∠BOF + ∠BOD,
所以160° = 28° + 8° + 2(x + 20°),
解得x = 42°,即∠COG = 42°.
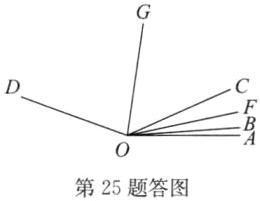
当OF在OB的左侧时,如答图.
设∠COG = x,则∠BOG = x + 20°,
因为OF平分∠AOC,OG平分∠BOD,
所以∠AOF = ∠FOC = 20° - 8° = 12°,∠BOD = 2(x + 20°).
因为∠AOD = ∠AOB + ∠BOD,
所以160° = 12° - 8° + 2(x + 20°),解得x = 58°,
即∠COG = 58°.
综上,∠COG的度数为42°或58°.
(1) 80°
(2)解:因为OF平分∠AOC,OG平分∠BOD,
所以∠FOC = $\frac{1}{2}$∠AOC,∠BOG = $\frac{1}{2}$∠BOD,
所以∠FOG = ∠FOC + ∠BOG - ∠BOC = $\frac{1}{2}$∠AOC + $\frac{1}{2}$∠BOD - ∠BOC = $\frac{1}{2}$(∠AOC + ∠BOD) - ∠BOC = $\frac{1}{2}$(∠AOD + ∠BOC) - ∠BOC = $\frac{1}{2}$(∠AOD - ∠BOC) = $\frac{1}{2}$×(160° - 20°) = 70°.
(3)解:当OF在OB的右侧时,如题图②.
设∠COG = x,则∠BOG = x + 20°.
因为OF平分∠AOC,OG平分∠BOD,
所以∠AOF = ∠FOC = 20° + 8° = 28°,∠BOD = 2(x + 20°).
因为∠AOD = ∠AOF + ∠BOF + ∠BOD,
所以160° = 28° + 8° + 2(x + 20°),
解得x = 42°,即∠COG = 42°.
当OF在OB的左侧时,如答图.
设∠COG = x,则∠BOG = x + 20°,
因为OF平分∠AOC,OG平分∠BOD,
所以∠AOF = ∠FOC = 20° - 8° = 12°,∠BOD = 2(x + 20°).
因为∠AOD = ∠AOB + ∠BOD,
所以160° = 12° - 8° + 2(x + 20°),解得x = 58°,
即∠COG = 58°.
综上,∠COG的度数为42°或58°.
