10.瑞士中学教师巴尔末成功地从光谱数据$\frac{9}{5}$,$\frac{4}{3}$,$\frac{25}{21}$,$\frac{9}{8}$,$\frac{49}{45}$,...中得到巴尔末公式,从而打开了光谱奥妙的大门,按此规律,第10个数据是
$\frac{36}{35}$
.答案：$ \frac{36}{35} $
解析：
将数据统一形式：$\frac{9}{5}$，$\frac{16}{12}$，$\frac{25}{21}$，$\frac{36}{32}$，$\frac{49}{45}$，...
分子：$9=3^2$，$16=4^2$，$25=5^2$，$36=6^2$，$49=7^2$，...，规律为$(n+2)^2$（$n$为正整数）
分母：$5=3^2-4$，$12=4^2-4$，$21=5^2-4$，$32=6^2-4$，$45=7^2-4$，...，规律为$(n+2)^2-4$
第10个数据，$n=10$，分子：$(10+2)^2=144$，分母：$(10+2)^2-4=140$，故第10个数据是$\frac{144}{140}=\frac{36}{35}$
答案：$\frac{36}{35}$
分子：$9=3^2$，$16=4^2$，$25=5^2$，$36=6^2$，$49=7^2$，...，规律为$(n+2)^2$（$n$为正整数）
分母：$5=3^2-4$，$12=4^2-4$，$21=5^2-4$，$32=6^2-4$，$45=7^2-4$，...，规律为$(n+2)^2-4$
第10个数据，$n=10$，分子：$(10+2)^2=144$，分母：$(10+2)^2-4=140$，故第10个数据是$\frac{144}{140}=\frac{36}{35}$
答案：$\frac{36}{35}$
11.别是∠α,∠β,若∠α= ∠β+20°,则∠β=
$35^{\circ}$
.答案：$35^{\circ}$
解析：
由图可知，∠α与∠β组成一个平角的补角，即∠α + ∠β = 90°。
已知∠α = ∠β + 20°，代入得：
∠β + 20° + ∠β = 90°
2∠β = 70°
∠β = 35°
35°
已知∠α = ∠β + 20°，代入得：
∠β + 20° + ∠β = 90°
2∠β = 70°
∠β = 35°
35°
12.(12分)已知关于x的方程m-m(x+3)= 2x的解与方程3y+7=-2(y-1)的解相等,求m的值.
答案：解: 解方程 $3y + 7 = -2(y - 1)$, 得 $y = -1$, 即方程 $m - m(x + 3) = 2x$ 的解为 $x = -1$, 把 $x = -1$ 代入方程 $m - m(x + 3) = 2x$, 得 $m - 2m = -2$, 解得 $m = 2$.
解析：
解：解方程 $3y + 7 = -2(y - 1)$，
去括号得：$3y + 7 = -2y + 2$，
移项得：$3y + 2y = 2 - 7$，
合并同类项得：$5y = -5$，
系数化为1得：$y = -1$。
因为关于$x$的方程$m - m(x + 3) = 2x$的解与上述方程的解相等，所以$x = -1$。
把$x = -1$代入方程$m - m(x + 3) = 2x$，
得：$m - m(-1 + 3) = 2×(-1)$，
即$m - 2m = -2$，
合并同类项得：$-m = -2$，
系数化为1得：$m = 2$。
故$m$的值为$2$。
去括号得：$3y + 7 = -2y + 2$，
移项得：$3y + 2y = 2 - 7$，
合并同类项得：$5y = -5$，
系数化为1得：$y = -1$。
因为关于$x$的方程$m - m(x + 3) = 2x$的解与上述方程的解相等，所以$x = -1$。
把$x = -1$代入方程$m - m(x + 3) = 2x$，
得：$m - m(-1 + 3) = 2×(-1)$，
即$m - 2m = -2$，
合并同类项得：$-m = -2$，
系数化为1得：$m = 2$。
故$m$的值为$2$。
13.(15分)(2024.秦淮区一模)新“龟兔赛跑”故事.兔子和乌龟从同一起点同时出发,匀速奔向终点.兔子的速度是乌龟速度的50倍
一段时间后,兔子到达途中某处,睡了70min,醒来后,它保持原速奔跑,恰好和乌龟同时到达终点.
(1)设乌龟的速度为xm/min,其奔跑的时间为tmin,则由虚线框内的文字可知兔子的速度是
(2)求(1)中t的值.
一段时间后,兔子到达途中某处,睡了70min,醒来后,它保持原速奔跑,恰好和乌龟同时到达终点.
(1)设乌龟的速度为xm/min,其奔跑的时间为tmin,则由虚线框内的文字可知兔子的速度是
50x
m/min,由题中的两个“同时"可知兔子奔跑的时间为t - 70
min;(2)求(1)中t的值.
解: 根据题意, 得 $x \cdot t = 50x \cdot (t - 70)$, 即 $t = 50(t - 70)$, 解得 $t = \frac{500}{7}$.
答案：(1) $50x$ $(t - 70)$ (2) 解: 根据题意, 得 $x \cdot t = 50x \cdot (t - 70)$, 即 $t = 50(t - 70)$, 解得 $t = \frac{500}{7}$.
解析：
(1) $50x$；$(t - 70)$
(2) 解：根据题意，得 $x \cdot t = 50x \cdot (t - 70)$
两边同时除以 $x$（$x \neq 0$），得 $t = 50(t - 70)$
展开得 $t = 50t - 3500$
移项得 $50t - t = 3500$
合并同类项得 $49t = 3500$
解得 $t = \frac{3500}{49} = \frac{500}{7}$
(2) 解：根据题意，得 $x \cdot t = 50x \cdot (t - 70)$
两边同时除以 $x$（$x \neq 0$），得 $t = 50(t - 70)$
展开得 $t = 50t - 3500$
移项得 $50t - t = 3500$
合并同类项得 $49t = 3500$
解得 $t = \frac{3500}{49} = \frac{500}{7}$
14.(18分)如图,M是线段AB上一定点,AB= 12cm,C,D两点分别从点M,B同时出发,以
1cm/s,3cm/s的速度沿直线BA向左运动(点C在线段AM上,点D在线段BM上).
(1)若AM= 4cm,当点C,D运动了2s时,AC= ______cm,DM= ______cm.
(2)若点C,D运动时,总有MD= 3AC.
①求线段AM的长;
②若N是直线AB上一点,且AN-BN= MN,求$\frac{MN}{AB}$的值.
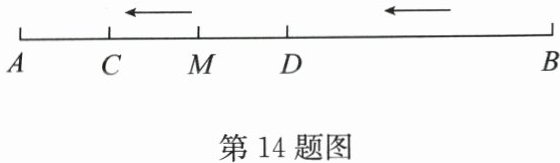
1cm/s,3cm/s的速度沿直线BA向左运动(点C在线段AM上,点D在线段BM上).
(1)若AM= 4cm,当点C,D运动了2s时,AC= ______cm,DM= ______cm.
(2)若点C,D运动时,总有MD= 3AC.
①求线段AM的长;
②若N是直线AB上一点,且AN-BN= MN,求$\frac{MN}{AB}$的值.
答案：
(1) 2 2 (2) 解: ① 由 $MD = 3AC$, 可设 $AC = x \text{ cm}$, $MD = 3x \text{ cm}$, 设运动时间为 $t \text{ s}$, 则 $MC = t \text{ cm}$, $BD = 3t \text{ cm}$, 所以 $AM = (x + t) \text{ cm}$, $AB = AC + CM + MD + BD = x + t + 3x + 3t = (4x + 4t) \text{ cm}$. 因为 $AB = 12 \text{ cm}$, 所以 $4x + 4t = 12$, 所以 $x + t = 3$, 即 $AM = 3 \text{ cm}$. ② 当点 $N$ 在线段 $AB$ 上时, 如答图①.
因为 $AN - BN = MN$, $AN - AM = MN$, 所以 $BN = AM = 3 \text{ cm}$, $MN = AB - AM - BN = 6 \text{ cm}$, 所以 $ \frac{MN}{AB} = \frac{1}{2} $. 当点 $N$ 在线段 $AB$ 的延长线上时, 如答图②. 
因为 $AN - BN = MN$, $AN - BN = AB$, 所以 $MN = AB$, 即 $ \frac{MN}{AB} = 1$. 综上, $ \frac{MN}{AB} $ 的值为 $ \frac{1}{2} $ 或 1.
(1) 2 2 (2) 解: ① 由 $MD = 3AC$, 可设 $AC = x \text{ cm}$, $MD = 3x \text{ cm}$, 设运动时间为 $t \text{ s}$, 则 $MC = t \text{ cm}$, $BD = 3t \text{ cm}$, 所以 $AM = (x + t) \text{ cm}$, $AB = AC + CM + MD + BD = x + t + 3x + 3t = (4x + 4t) \text{ cm}$. 因为 $AB = 12 \text{ cm}$, 所以 $4x + 4t = 12$, 所以 $x + t = 3$, 即 $AM = 3 \text{ cm}$. ② 当点 $N$ 在线段 $AB$ 上时, 如答图①.
因为 $AN - BN = MN$, $AN - AM = MN$, 所以 $BN = AM = 3 \text{ cm}$, $MN = AB - AM - BN = 6 \text{ cm}$, 所以 $ \frac{MN}{AB} = \frac{1}{2} $. 当点 $N$ 在线段 $AB$ 的延长线上时, 如答图②. 因为 $AN - BN = MN$, $AN - BN = AB$, 所以 $MN = AB$, 即 $ \frac{MN}{AB} = 1$. 综上, $ \frac{MN}{AB} $ 的值为 $ \frac{1}{2} $ 或 1.