1. (2024·泰兴月考)如果$a$,$b$,$c$是正数,且满足$a + b + c = 1$,$\frac{1}{a + b} + \frac{1}{b + c} + \frac{1}{a + c} = 6$,那么$\frac{a}{b + c} + \frac{b}{a + c} + \frac{c}{a + b}$的值为(
A.$-2$
B.$2$
C.$3$
D.$\frac{1}{3}$
C
)A.$-2$
B.$2$
C.$3$
D.$\frac{1}{3}$
答案:C
解析:
解:因为$a + b + c = 1$,所以$a = 1 - (b + c)$,$b = 1 - (a + c)$,$c = 1 - (a + b)$。
$\begin{aligned}\frac{a}{b + c} + \frac{b}{a + c} + \frac{c}{a + b}&=\frac{1 - (b + c)}{b + c} + \frac{1 - (a + c)}{a + c} + \frac{1 - (a + b)}{a + b}\\&=\left(\frac{1}{b + c} - 1\right) + \left(\frac{1}{a + c} - 1\right) + \left(\frac{1}{a + b} - 1\right)\\&=\left(\frac{1}{a + b} + \frac{1}{b + c} + \frac{1}{a + c}\right) - 3\end{aligned}$
已知$\frac{1}{a + b} + \frac{1}{b + c} + \frac{1}{a + c} = 6$,代入上式得:
$6 - 3 = 3$
答案:C
$\begin{aligned}\frac{a}{b + c} + \frac{b}{a + c} + \frac{c}{a + b}&=\frac{1 - (b + c)}{b + c} + \frac{1 - (a + c)}{a + c} + \frac{1 - (a + b)}{a + b}\\&=\left(\frac{1}{b + c} - 1\right) + \left(\frac{1}{a + c} - 1\right) + \left(\frac{1}{a + b} - 1\right)\\&=\left(\frac{1}{a + b} + \frac{1}{b + c} + \frac{1}{a + c}\right) - 3\end{aligned}$
已知$\frac{1}{a + b} + \frac{1}{b + c} + \frac{1}{a + c} = 6$,代入上式得:
$6 - 3 = 3$
答案:C
2. (1)已知$x^{2} + 2y = 5$,求代数式$-3x^{2} - 6y + 21$的值;
(2)已知$a - 2b = 3$,$2b - c = -5$,$c - d = 10$,求$(a - c) + (2b - d) - (2b - c)$的值。
(2)已知$a - 2b = 3$,$2b - c = -5$,$c - d = 10$,求$(a - c) + (2b - d) - (2b - c)$的值。
答案:解: (1) 因为 $ x^{2}+2 y=5 $,所以原式 $ =-3\left(x^{2}+2 y\right)+21=-3 × 5+21=6 $。(2) 因为 $ a-2 b=3,2 b-c=-5, c-d=10 $,所以 $ a-c=a-2 b+2 b-c=3+(-5)=-2,2 b-d=2 b-c+c-d=-5+10=5 $,所以原式 $ =-2+5-(-5)=8 $。
解析:
(1) 解:因为 $x^{2} + 2y = 5$,所以$-3x^{2} - 6y + 21 = -3(x^{2} + 2y) + 21 = -3×5 + 21 = 6$。
(2) 解:因为 $a - 2b = 3$,$2b - c = -5$,$c - d = 10$,所以$a - c = (a - 2b) + (2b - c) = 3 + (-5) = -2$,$2b - d = (2b - c) + (c - d) = -5 + 10 = 5$,则$(a - c) + (2b - d) - (2b - c) = -2 + 5 - (-5) = 8$。
(2) 解:因为 $a - 2b = 3$,$2b - c = -5$,$c - d = 10$,所以$a - c = (a - 2b) + (2b - c) = 3 + (-5) = -2$,$2b - d = (2b - c) + (c - d) = -5 + 10 = 5$,则$(a - c) + (2b - d) - (2b - c) = -2 + 5 - (-5) = 8$。
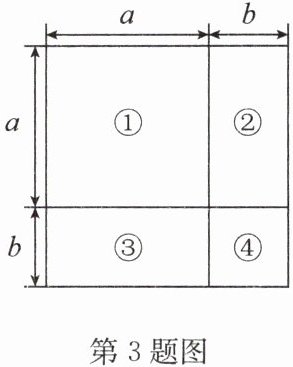
3. 操作与思考:有一张边长为$a$的正方形桌面,根据实际需要,要将正方形的边长增加$b$,从而得到一个更大的正方形,木工师傅设计了如图所示的方案。
(1)方案中大正方形的边长是
(2)小明发现:方案中大正方形的面积还可以用四个小四边形的面积和表示为
(3)你有什么发现?请用数学式子表达:
(4)利用(3)的结论计算$20.18^{2} + 2×20.18×19.82 + 19.82^{2}$的值。
(1)方案中大正方形的边长是
$a+b$
,所以面积为$(a+b)^{2}$
;(2)小明发现:方案中大正方形的面积还可以用四个小四边形的面积和表示为
$a^{2}+2ab+b^{2}$
;(3)你有什么发现?请用数学式子表达:
$(a+b)^{2}=a^{2}+2ab+b^{2}$
;(4)利用(3)的结论计算$20.18^{2} + 2×20.18×19.82 + 19.82^{2}$的值。

解: 原式$=(20.18+19.82)^{2}=40^{2}=1600$。
答案:(1) $ a+b $ $ (a+b)^{2} $(2) $ a^{2}+2 a b+b^{2} $(3) $ (a+b)^{2}=a^{2}+2 a b+b^{2} $(4) 解: 原式 $ =(20.18+19.82)^{2}=40^{2}=1600 $。