1. (2024·新吴区期末)如果单项式 $x^{2}y^{m + 2}$ 与 $x^{n}y$ 的和仍然是一个单项式,则 $m,n$ 的值是 (
A.$m = 2,n = 2$
B.$m = - 1,n = 2$
C.$m = - 2,n = 2$
D.$m = 2,n = - 1$
B
)A.$m = 2,n = 2$
B.$m = - 1,n = 2$
C.$m = - 2,n = 2$
D.$m = 2,n = - 1$
答案:B
解析:
解:因为两个单项式的和仍是单项式,所以它们是同类项。
同类项要求相同字母的指数相同,故:
$n = 2$,$m + 2 = 1$
解得$m = -1$,$n = 2$
答案:B
同类项要求相同字母的指数相同,故:
$n = 2$,$m + 2 = 1$
解得$m = -1$,$n = 2$
答案:B
2. 已知 $A= (m - 2)\,x^{n}y,B= \frac{2}{5}x^{2}y + 6$,无论 $x,y$ 为何值,总有 $A + B = 6$,则 $\frac{m}{n^{3}}= $
$\frac{1}{5}$
。答案:$\frac{1}{5}$ 点拨:由题意,得 $m - 2 = -\frac{2}{5},n = 2$,解得 $m = \frac{8}{5}$,所以 $\frac{m}{n^3} = \frac{\frac{8}{5}}{8} = \frac{1}{5}$.
解析:
解:因为无论$x,y$为何值,总有$A + B = 6$,
$A + B=(m - 2)x^{n}y+\frac{2}{5}x^{2}y + 6$,
所以$(m - 2)x^{n}y+\frac{2}{5}x^{2}y$的和为$0$,
则$m - 2=-\frac{2}{5}$,$n = 2$,
解得$m=\frac{8}{5}$,
所以$\frac{m}{n^{3}}=\frac{\frac{8}{5}}{2^{3}}=\frac{\frac{8}{5}}{8}=\frac{1}{5}$。
故答案为$\frac{1}{5}$。
$A + B=(m - 2)x^{n}y+\frac{2}{5}x^{2}y + 6$,
所以$(m - 2)x^{n}y+\frac{2}{5}x^{2}y$的和为$0$,
则$m - 2=-\frac{2}{5}$,$n = 2$,
解得$m=\frac{8}{5}$,
所以$\frac{m}{n^{3}}=\frac{\frac{8}{5}}{2^{3}}=\frac{\frac{8}{5}}{8}=\frac{1}{5}$。
故答案为$\frac{1}{5}$。
3. 定义:若 $x - y = m$,则称 $x$ 与 $y$ 是关于 $m$ 的相关数。
(1) 若 $5$ 与 $a$ 是关于 $2$ 的相关数,则 $a= $
(2) 若 $A$ 与 $B$ 是关于 $m$ 的相关数,且 $A = 3mn - 5m + n + 6$,$B$ 的值与 $m$ 的取值无关,求 $B$ 的值。
(1) 若 $5$ 与 $a$ 是关于 $2$ 的相关数,则 $a= $
3
;(2) 若 $A$ 与 $B$ 是关于 $m$ 的相关数,且 $A = 3mn - 5m + n + 6$,$B$ 的值与 $m$ 的取值无关,求 $B$ 的值。
解:因为 $A - B = m,A = 3mn - 5m + n + 6$,所以 $3mn - 5m + n + 6 - B = m$,所以 $B = 3mn - 5m + n + 6 - m = 3mn - 6m + n + 6 = (3n - 6)m + n + 6$.因为 B 的值与 m 的取值无关,所以 $3n - 6 = 0$,所以 $n = 2$,所以 $B = 2 + 6 = 8$.
答案:(1)3
(2)解:因为 $A - B = m,A = 3mn - 5m + n + 6$,所以 $3mn - 5m + n + 6 - B = m$,所以 $B = 3mn - 5m + n + 6 - m = 3mn - 6m + n + 6 = (3n - 6)m + n + 6$.因为 B 的值与 m 的取值无关,所以 $3n - 6 = 0$,所以 $n = 2$,所以 $B = 2 + 6 = 8$.
(2)解:因为 $A - B = m,A = 3mn - 5m + n + 6$,所以 $3mn - 5m + n + 6 - B = m$,所以 $B = 3mn - 5m + n + 6 - m = 3mn - 6m + n + 6 = (3n - 6)m + n + 6$.因为 B 的值与 m 的取值无关,所以 $3n - 6 = 0$,所以 $n = 2$,所以 $B = 2 + 6 = 8$.
1. 化简$-[-(-a^{2})-b^{2}]-[+(-b^{2})]$,结果是 (
A.$2b^{2}-a^{2}$
B.$-a^{2}$
C.$a^{2}$
D.$a^{2}-2b^{2}$
A
)A.$2b^{2}-a^{2}$
B.$-a^{2}$
C.$a^{2}$
D.$a^{2}-2b^{2}$
答案:A
解析:
解:$-[-(-a^{2})-b^{2}]-[+(-b^{2})]$
$=-(a^{2}-b^{2})-(-b^{2})$
$=-a^{2}+b^{2}+b^{2}$
$=-a^{2}+2b^{2}$
$=2b^{2}-a^{2}$
A
$=-(a^{2}-b^{2})-(-b^{2})$
$=-a^{2}+b^{2}+b^{2}$
$=-a^{2}+2b^{2}$
$=2b^{2}-a^{2}$
A
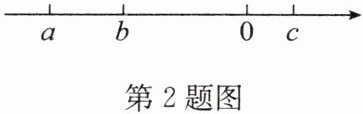
2. 已知有理数$a$,$b$,$c$对应的点在数轴上的位置如图所示,且$|b|>$ $|c|$,化简:$2|c-b|-|a+c|= $
$ 3 c - 2 b + a $
。
答案:$ 3 c - 2 b + a $
解析:
由数轴可知:$a < b < 0 < c$,且$|b| > |c|$。
因为$c > b$,所以$c - b > 0$,则$|c - b| = c - b$,故$2|c - b| = 2(c - b) = 2c - 2b$。
因为$a < 0$,$c > 0$,且$|a| > |c|$(由$a < b < 0$,$|b| > |c|$可得),所以$a + c < 0$,则$|a + c| = - (a + c) = -a - c$。
所以$2|c - b| - |a + c| = (2c - 2b) - (-a - c) = 2c - 2b + a + c = 3c - 2b + a$。
$3c - 2b + a$
因为$c > b$,所以$c - b > 0$,则$|c - b| = c - b$,故$2|c - b| = 2(c - b) = 2c - 2b$。
因为$a < 0$,$c > 0$,且$|a| > |c|$(由$a < b < 0$,$|b| > |c|$可得),所以$a + c < 0$,则$|a + c| = - (a + c) = -a - c$。
所以$2|c - b| - |a + c| = (2c - 2b) - (-a - c) = 2c - 2b + a + c = 3c - 2b + a$。
$3c - 2b + a$
3. 已知$a^{2}+ab= 3$,$ab+b^{2}= 6$,求下列代数式的值:
(1)$a^{2}-b^{2}$; (2)$a^{2}+4ab+3b^{2}$。
(1)$a^{2}-b^{2}$; (2)$a^{2}+4ab+3b^{2}$。
答案:(1)因为 $ a ^ { 2 } + a b = 3 $,$ a b + b ^ { 2 } = 6 $,所以 $ a ^ { 2 } - b ^ { 2 } = ( a ^ { 2 } + a b ) - ( a b + b ^ { 2 } ) = 3 - 6 = - 3 $。(2)因为 $ a ^ { 2 } + a b = 3 $,$ a b + b ^ { 2 } = 6 $,所以 $ a ^ { 2 } + 4 a b + 3 b ^ { 2 } = ( a ^ { 2 } + a b ) + 3 ( a b + b ^ { 2 } ) = 3 + 18 = 21 $。