1. 观察如图所示的图形,它们是按一定规律排列的,依照此规律,第n个图形中的实心点一共有
$\frac{3n^{2}+3n}{2}$
个.答案:$\frac{3n^{2}+3n}{2}$ 点拨:第 1 个图形有 $3 = 3×1 = 3$(个)点,第 2 个图形有 $3 + 6 = 3×(1 + 2) = 9$(个)点,第 3 个图形有 $3 + 6 + 9 = 3×(1 + 2 + 3) = 18$(个)点,……第 n 个图形有 $3 + 6 + 9 + \cdots + 3n = 3×(1 + 2 + 3 + \cdots + n) = \frac{3n(n + 1)}{2} = \frac{3n^{2} + 3n}{2}$(个)点.
解析:
第1个图形有 $3 = 3×1$ 个点;
第2个图形有 $3 + 6 = 3×(1 + 2)$ 个点;
第3个图形有 $3 + 6 + 9 = 3×(1 + 2 + 3)$ 个点;
……
第n个图形有 $3 + 6 + 9 + \cdots + 3n = 3×(1 + 2 + 3 + \cdots + n)$ 个点。
因为 $1 + 2 + 3 + \cdots + n = \frac{n(n + 1)}{2}$,所以第n个图形中的实心点一共有 $3×\frac{n(n + 1)}{2} = \frac{3n(n + 1)}{2} = \frac{3n^2 + 3n}{2}$ 个。
$\frac{3n^2 + 3n}{2}$
第2个图形有 $3 + 6 = 3×(1 + 2)$ 个点;
第3个图形有 $3 + 6 + 9 = 3×(1 + 2 + 3)$ 个点;
……
第n个图形有 $3 + 6 + 9 + \cdots + 3n = 3×(1 + 2 + 3 + \cdots + n)$ 个点。
因为 $1 + 2 + 3 + \cdots + n = \frac{n(n + 1)}{2}$,所以第n个图形中的实心点一共有 $3×\frac{n(n + 1)}{2} = \frac{3n(n + 1)}{2} = \frac{3n^2 + 3n}{2}$ 个。
$\frac{3n^2 + 3n}{2}$
2. 若$m_{1},m_{2},...,m_{2025}$是从1,2这两个数中取值的一列数,$(m_{1}-1)+(m_{2}-1)^{2}+(m_{3}-1)^{3}+... +(m_{2025}-1)^{2025}= 1000$,则在$m_{1},m_{2},...,m_{2025}$中,取值为1的个数为
1025
.答案:1025 点拨:因为 $(m_{1} - 1) + (m_{2} - 1)^{2} + (m_{3} - 1)^{3} + \cdots + (m_{2025} - 1)^{2025} = 1000$,所以 $m_{1},m_{2},\cdots,m_{2025}$ 中有 1000 个数取值为 2,所以取值为 1 的个数为 $2025 - 1000 = 1025$.
解析:
解:设这列数中取值为1的个数为$x$,取值为2的个数为$y$。
因为这列数共有2025个数,所以$x + y = 2025$。
当$m_i = 1$时,$(m_i - 1)^i = (1 - 1)^i = 0^i = 0$($i$为正整数);
当$m_i = 2$时,$(m_i - 1)^i = (2 - 1)^i = 1^i = 1$($i$为正整数)。
已知$(m_{1}-1)+(m_{2}-1)^{2}+(m_{3}-1)^{3}+\cdots +(m_{2025}-1)^{2025}=1000$,而该式的值等于取值为2的数的个数,即$y = 1000$。
将$y = 1000$代入$x + y = 2025$,得$x = 2025 - 1000 = 1025$。
故取值为1的个数为$1025$。
因为这列数共有2025个数,所以$x + y = 2025$。
当$m_i = 1$时,$(m_i - 1)^i = (1 - 1)^i = 0^i = 0$($i$为正整数);
当$m_i = 2$时,$(m_i - 1)^i = (2 - 1)^i = 1^i = 1$($i$为正整数)。
已知$(m_{1}-1)+(m_{2}-1)^{2}+(m_{3}-1)^{3}+\cdots +(m_{2025}-1)^{2025}=1000$,而该式的值等于取值为2的数的个数,即$y = 1000$。
将$y = 1000$代入$x + y = 2025$,得$x = 2025 - 1000 = 1025$。
故取值为1的个数为$1025$。
3.【规律探索】用同样大小的两种不同颜色的正方形纸片,按如图所示方式拼成长方形.
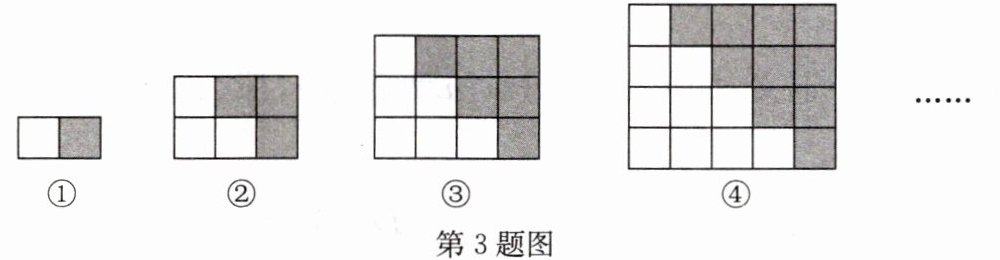
第①个图形中有2张正方形纸片;
第②个图形中有$2×(1+2)= 2+4= 6$(张)正方形纸片;
第③个图形中有$2×(1+2+3)= 2+4+6= 12$(张)正方形纸片;
第④个图形中有$2×(1+2+3+4)= 2+4+6+8= 20$(张)正方形纸片;
……
请你观察上述图形与算式,解答下列问题:
【规律归纳】
(1)第⑦个图形中有____张正方形纸片.(直接写出结果)
(2)根据上面的发现,我们可以猜想:$2+4+6+... +2n= $____.(用含n的代数式表示)
【规律应用】
(3)根据你发现的规律计算:
①$2+4+6+... +2000;$
②$202+204+206+... +600.$
[答案]:3. (1)
(2)
(3)解:①
②

第①个图形中有2张正方形纸片;
第②个图形中有$2×(1+2)= 2+4= 6$(张)正方形纸片;
第③个图形中有$2×(1+2+3)= 2+4+6= 12$(张)正方形纸片;
第④个图形中有$2×(1+2+3+4)= 2+4+6+8= 20$(张)正方形纸片;
……
请你观察上述图形与算式,解答下列问题:
【规律归纳】
(1)第⑦个图形中有____张正方形纸片.(直接写出结果)
(2)根据上面的发现,我们可以猜想:$2+4+6+... +2n= $____.(用含n的代数式表示)
【规律应用】
(3)根据你发现的规律计算:
①$2+4+6+... +2000;$
②$202+204+206+... +600.$
[答案]:3. (1)
56
(2)
$n(n + 1)$
(3)解:①
$2 + 4 + 6 + \cdots + 2000 = 1000×1001 = 1001000$
.②
$202 + 204 + 206 + \cdots + 600 = (2 + 4 + 6 + \cdots + 600) - (2 + 4 + 6 + \cdots + 200) = 300×301 - 100×101 = 80200$
.答案:3. (1)56
(2) $n(n + 1)$
(3)解:① $2 + 4 + 6 + \cdots + 2000 = 1000×1001 = 1001000$.
② $202 + 204 + 206 + \cdots + 600 = (2 + 4 + 6 + \cdots + 600) - (2 + 4 + 6 + \cdots + 200) = 300×301 - 100×101 = 80200$.
(2) $n(n + 1)$
(3)解:① $2 + 4 + 6 + \cdots + 2000 = 1000×1001 = 1001000$.
② $202 + 204 + 206 + \cdots + 600 = (2 + 4 + 6 + \cdots + 600) - (2 + 4 + 6 + \cdots + 200) = 300×301 - 100×101 = 80200$.