1. 平面上不重合的两点确定一条直线,不同的 3 个点最多可确定 3 条直线,若平面上不同的 n 个点最多可确定 21 条直线,则 n 的值为(
A.5
B.6
C.7
D.8
C
)A.5
B.6
C.7
D.8
答案:C
解析:
解:平面上不同的$n$个点,每两个点确定一条直线,最多可确定直线的条数为$\frac{n(n - 1)}{2}$。
由题意得$\frac{n(n - 1)}{2}=21$,
整理得$n^2 - n - 42 = 0$,
因式分解得$(n - 7)(n + 6)=0$,
解得$n = 7$或$n=-6$(舍去),
所以$n = 7$。
答案:C
由题意得$\frac{n(n - 1)}{2}=21$,
整理得$n^2 - n - 42 = 0$,
因式分解得$(n - 7)(n + 6)=0$,
解得$n = 7$或$n=-6$(舍去),
所以$n = 7$。
答案:C
2. 如图是某住宅小区平面图,点 B 是“菜鸟驿站”的位置,其余各点为居民楼,图中各条线为小区内的小路,从居民楼点 A 到“菜鸟驿站”点 B 的最短路径是(
A.$ A - C - G - E - B $
B.$ A - C - E - B $
C.$ A - D - G - E - B $
D.$ A - F - E - B $
D
)A.$ A - C - G - E - B $
B.$ A - C - E - B $
C.$ A - D - G - E - B $
D.$ A - F - E - B $
答案:D
解析:
解:根据“两点之间,线段最短”,观察各选项路径:
A选项:A - C - G - E - B,路径包含折线和曲线,长度较长。
B选项:A - C - E - B,AC + CE为折线,AE为线段,AC + CE > AE。
C选项:A - D - G - E - B,路径包含曲线和折线,长度最长。
D选项:A - F - E - B,AF + FE = AE,AE + EB为线段连接,路径最短。
结论:D
A选项:A - C - G - E - B,路径包含折线和曲线,长度较长。
B选项:A - C - E - B,AC + CE为折线,AE为线段,AC + CE > AE。
C选项:A - D - G - E - B,路径包含曲线和折线,长度最长。
D选项:A - F - E - B,AF + FE = AE,AE + EB为线段连接,路径最短。
结论:D
3. 如图,有三个住宅小区 A,B,C 在一条大道上(即 A,B,C 三点共线),某公司在 A,B,C 各小区分别住有职工 30 人,15 人,10 人。已知 $ AB = 100 $ 米,$ BC = 200 $ 米,为了方便职工上下班,该公司的班车打算在某小区设一个停靠点,为使所有的人步行到停靠点的路程之和最小,那么该停靠点的位置应该设在哪个小区?
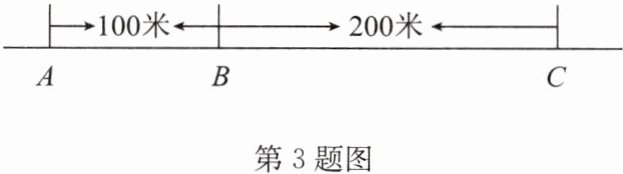

答案:解:以小区 A 为停靠点,则所有人的路程的和为 $$15×100 + 10×300 = 4500$$ (米),
以小区 B 为停靠点,则所有人的路程的和为 $$30×100 + 10×200 = 5000$$ (米),
以小区 C 为停靠点,则所有人的路程的和为 $$30×300 + 15×200 = 12000$$ (米),
因为 $$4500 < 5000 < 12000$$,
所以该停靠点的位置应设在小区 A.
以小区 B 为停靠点,则所有人的路程的和为 $$30×100 + 10×200 = 5000$$ (米),
以小区 C 为停靠点,则所有人的路程的和为 $$30×300 + 15×200 = 12000$$ (米),
因为 $$4500 < 5000 < 12000$$,
所以该停靠点的位置应设在小区 A.