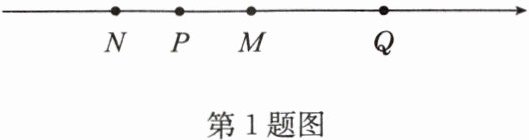
1. 如图,数轴上 M,N,P,Q 四点表示的数都是整数,且 M 为线段 NQ 的中点,P 为线段 NM 的中点。若点 M 表示的整数是 a,点 N 表示的整数是 b,且 $ b - 2 a = 0 $,则数轴上的原点是(
A.M
B.N
C.P
D.Q
D
)
A.M
B.N
C.P
D.Q
答案:D
解析:
解:
∵点M表示的整数是a,点N表示的整数是b,且$b - 2a = 0$,
∴$b = 2a$。
∵M为线段NQ的中点,
∴点Q表示的数为$2a - b = 2a - 2a = 0$。
∴数轴上的原点是Q。
答案:D
∵点M表示的整数是a,点N表示的整数是b,且$b - 2a = 0$,
∴$b = 2a$。
∵M为线段NQ的中点,
∴点Q表示的数为$2a - b = 2a - 2a = 0$。
∴数轴上的原点是Q。
答案:D
2. (2024·启东月考)两根木条,一根长 10 cm,另一根长 8 cm,将它们一端重合且放在同一条直线上,此时两根木条的中点之间的距离为
1或9
cm。答案:1或9
解析:
解:情况一:两根木条同向放置
10cm木条中点到重合端距离:10÷2=5cm
8cm木条中点到重合端距离:8÷2=4cm
中点距离:5-4=1cm
情况二:两根木条反向放置
中点距离:5+4=9cm
答案:1或9
10cm木条中点到重合端距离:10÷2=5cm
8cm木条中点到重合端距离:8÷2=4cm
中点距离:5-4=1cm
情况二:两根木条反向放置
中点距离:5+4=9cm
答案:1或9
3. 已知 $ x = - 3 $ 是关于 x 的方程 $ ( k + 3 ) x + 2 = 3 x - 2 k $ 的解。
(1) 求 k 的值;
(2) 已知线段 $ AB = 6 \mathrm { cm } $,C 是直线 AB 上一点,且 $ B C = k A C $,若 D 是 AC 的中点,求线段 CD 的长。
(1) 求 k 的值;
(2) 已知线段 $ AB = 6 \mathrm { cm } $,C 是直线 AB 上一点,且 $ B C = k A C $,若 D 是 AC 的中点,求线段 CD 的长。
答案:
解:(1)把 $ x = -3 $ 代入方程 $ (k + 3)x + 2 = 3x - 2k $,得 $ -3(k + 3) + 2 = -9 - 2k $,解得 $ k = 2 $。
(2)由(1)知 $ k = 2 $,所以 $ BC = 2AC $。
当点 $ C $ 在线段 $ AB $ 上时,如答图①,
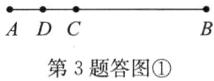
因为 $ AB = 6 \text{ cm} $,$ BC = 2AC $,
所以 $ AC = 2 \text{ cm} $,$ BC = 4 \text{ cm} $。
因为 $ D $ 为 $ AC $ 的中点,所以 $ CD = \frac{1}{2}AC = 1 \text{ cm} $;
当点 $ C $ 在 $ BA $ 的延长线上时,如答图②,

因为 $ BC = 2AC $,$ AB = 6 \text{ cm} $,所以 $ AC = 6 \text{ cm} $。
因为 $ D $ 为 $ AC $ 的中点,所以 $ CD = \frac{1}{2}AC = 3 \text{ cm} $。
综上,$ CD $ 的长为 $ 1 \text{ cm} $ 或 $ 3 \text{ cm} $。
解:(1)把 $ x = -3 $ 代入方程 $ (k + 3)x + 2 = 3x - 2k $,得 $ -3(k + 3) + 2 = -9 - 2k $,解得 $ k = 2 $。
(2)由(1)知 $ k = 2 $,所以 $ BC = 2AC $。
当点 $ C $ 在线段 $ AB $ 上时,如答图①,

因为 $ AB = 6 \text{ cm} $,$ BC = 2AC $,
所以 $ AC = 2 \text{ cm} $,$ BC = 4 \text{ cm} $。
因为 $ D $ 为 $ AC $ 的中点,所以 $ CD = \frac{1}{2}AC = 1 \text{ cm} $;
当点 $ C $ 在 $ BA $ 的延长线上时,如答图②,

因为 $ BC = 2AC $,$ AB = 6 \text{ cm} $,所以 $ AC = 6 \text{ cm} $。
因为 $ D $ 为 $ AC $ 的中点,所以 $ CD = \frac{1}{2}AC = 3 \text{ cm} $。
综上,$ CD $ 的长为 $ 1 \text{ cm} $ 或 $ 3 \text{ cm} $。